题目内容
如图所示，△ABC≌△CDA，AC=7 cm，AB=5 cm，BC=8 cm，则AD的长是（ ）
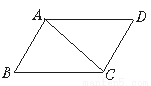
A.7 cm B.5 cm C.8 cm D.无法确定
C
【解析】
试题分析：根据全等三角形的性质即可得到结果.
∵△ABC≌△CDA，
∴BC=AD=8 cm，
故选C.
练习册系列答案
备战中考寒假系列答案
相关题目
如图,下列说法错误的是( )
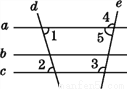
A. 若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
C
【解析】试题分析：根据平行线的判定进行判断即可．
【解析】
A、若a∥b，b∥c，则a∥c，利用了平行公理，正确；
B、若∠1=∠2，则a∥c，利用了内错角相等，两直线平行，正确；
C、∠3=∠2，不能判断b∥c，错误；
D、若∠3+∠5=180°，则a∥c，利用同旁内角互补，两直线平行，正确；
故选C． 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
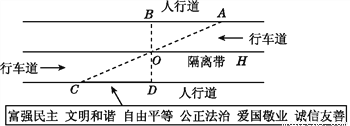
20米.
【解析】试题分析：已知AB∥CD，根据平行线的性质可得∠ABO=∠CDO，再由垂直的定义可得∠CDO=90°，可得OB⊥AB，根据相邻两平行线间的距离相等可得OD=OB，即可根据ASA定理判定△ABO≌△CDO，由全等三角形的性质即可得CD=AB=20m．
试题解析：∵AB∥CD，∴∠ABO=∠CDO，
∵OD⊥CD，∴∠CDO=90°，
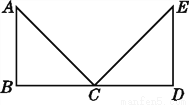
∴∠ABO=90°，即O... 如图，木工师傅在做完门框后，为防止变形常常象图中所示那样钉上两条斜拉的木条（图中的AB，CD两根木条），这样做是运用了三角形的（ ）
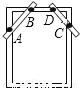
A. 全等性 B. 灵活性 C. 稳定性 D. 对称性
C
【解析】三角形具有稳定性，其他多边形不具有稳定性，把多边形分割成三角形则多边形的形状就不会改变，故这样做是运用了三角形的稳定性.
故选：C. 如图,已知△ABC≌△EDC,指出其对应边和对应角.
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析：△ABC≌△EDC，
∴AB的对应边是ED，AC的对应边是EC，BC的对应边是DC，
∠A的对应角是∠E，∠B的对应角是∠D，∠ACB的对应角是∠ECD. 下列说法正确的是（ ）
①用一张相纸冲洗出来的10张1寸相片是全等形；②我国国旗上的4颗小五角星是全等形；③所有的正方形是全等形；④全等形的面积一定相等．
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】能够完全重合的两个图形叫做全等形。
①正确，用一张相纸冲洗出来的10张1寸相片，各相片可以完全重合，故是全等形；
②正确，我国国旗上的4颗小五角星是全等形；
③错误，所有的正方形边长不一定一样，故不能完全重合，不能称都是全等形；
④正确，全等形可以完全重合，故其面积一定相等。
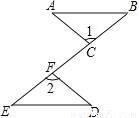
故选：C. 如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）
见解析
【解析】试题分析：先求出BC=EF，添加条件AC=DF，根据SAS推出两三角形全等即可．
AC=DF．
证明：∵BF=EC，
∴BF﹣CF=EC﹣CF，
∴BC=EF，
在△ABC和△DEF中
∴△ABC≌△DEF（SAS）． 若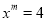
， 
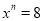，求
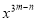的值。
8
【解析】试题分析：根据已知条件，逆用同底数幂的除法法则计算即可.
试题解析：
∵， ，
∴ 下列运算正确的是( )
A. 2x(x2＋3x－5)＝2x3＋3x－5 B. a6÷a2＝a3
C. (－2)－3＝－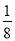
D. (a＋b)(a－b)＝(a－b)2
C
【解析】选项A,原式=2x3＋6x2－10x;选项B,原式=a4;选项C,原式=－;选项D，原式= a2-b2，故选C.