题目内容
已知抛物线y=a(x-2)2+9经过点(1,8).
(1)求a的值;
(2)若抛物线与x轴交于A,B两点,与y轴交于点C,求A,B,C的坐标;
(3)求△ABC的面积.
(1)求a的值;
(2)若抛物线与x轴交于A,B两点,与y轴交于点C,求A,B,C的坐标;
(3)求△ABC的面积.
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:计算题
分析:(1)根据二次函数图象上点的坐标特征得到a(1-2)2+9=8,然后解方程即可;
(2)由(1)得到抛物线解析式为y=-(x-2)2+9,根据抛物线与x轴的交点问题,解方程-(x-2)2+9=0即可得到A和B点坐标;利用y轴上点的坐标特征求自变量为0时的函数值即可得到C点坐标;
(3)根据三角形面积公式求解.
(2)由(1)得到抛物线解析式为y=-(x-2)2+9,根据抛物线与x轴的交点问题,解方程-(x-2)2+9=0即可得到A和B点坐标;利用y轴上点的坐标特征求自变量为0时的函数值即可得到C点坐标;
(3)根据三角形面积公式求解.
解答:解:(1)把(1,8)代入y=a(x-2)2+9得a(1-2)2+9=8,
解得a=-1;
(2)抛物线解析式为y=-(x-2)2+9,
当y=0时,-(x-2)2+9=0,解得x1=-1,x2=5,则A点和B点坐标为(-1,0)、(5,0);
当x=0时,y=-(x-2)2+9=-4+9=5,则C点坐标为(0,5);
(3)S△ABC=
×(5+1)×5=15.
解得a=-1;
(2)抛物线解析式为y=-(x-2)2+9,
当y=0时,-(x-2)2+9=0,解得x1=-1,x2=5,则A点和B点坐标为(-1,0)、(5,0);
当x=0时,y=-(x-2)2+9=-4+9=5,则C点坐标为(0,5);
(3)S△ABC=
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数图象上点的坐标特征.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 已知如图,△ACD与△BCE为等腰三角形,其中CA=CD,CB=CE,∠ACD=∠BCE=α,BD、AE交于点F,求∠BFE和∠AFC的度数.
已知如图,△ACD与△BCE为等腰三角形,其中CA=CD,CB=CE,∠ACD=∠BCE=α,BD、AE交于点F,求∠BFE和∠AFC的度数.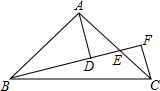 已知Rt△ABC中,AB=AC,∠BAC=90°,E是AC上一点,AD⊥BE于D,CF⊥BE于F,探究AD与DF的关系.
已知Rt△ABC中,AB=AC,∠BAC=90°,E是AC上一点,AD⊥BE于D,CF⊥BE于F,探究AD与DF的关系. 如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.
如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长. 作图:作图题
作图:作图题 作图题:已知线段a,b,求作:线段AB=a+2b (用直尺和圆规作图,保留作图痕迹,不写作法)
作图题:已知线段a,b,求作:线段AB=a+2b (用直尺和圆规作图,保留作图痕迹,不写作法)