题目内容
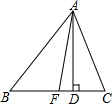如图，在△ABC中，AD，AE分别是BC边上的高和中线，AB=7cm，AC=4cm，BC=6cm，求DE的长．考点：勾股定理
专题：
分析：如图，设BD=λ，运用勾股定理列出关于λ的方程，求出λ即可解决问题．
解答：
解：如图，设BD=λ，则CD=6-λ；
∵AD⊥BC，
∴AD2=AB2-BD2，AD2=AC2-CD2，
∴72-λ2=42-（6-λ）2，
解得：λ=
，
∵AE是中线，
∴BE=
BC=3，
∴DE=λ-3=
．
解：如图，设BD=λ，则CD=6-λ；∵AD⊥BC，
∴AD2=AB2-BD2，AD2=AC2-CD2，
∴72-λ2=42-（6-λ）2，
解得：λ=
| 23 |
| 4 |
∵AE是中线，
∴BE=
| 1 |
| 2 |
∴DE=λ-3=
| 11 |
| 4 |
点评：该题主要考查了勾股定理、三角形中线的定义及其应用等几何知识点问题；应牢固掌握了勾股定理．
练习册系列答案
名校课堂系列答案
相关题目
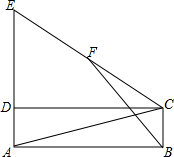如图，在矩形ABCD中，延长AD至E，使AE=AC，F为CE的中点，连接BF．
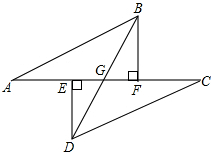如图，点A，E，F，C在同一条直线上，AE=CF，过点E，F分别作DE⊥AC，BF⊥AC，若AB=CD，求证：BD平分EF．下列命题中是真命题的是（ ）
| A、五边形的外角和等于360° |
| B、如果a+b＞0，那么ab＞0 |
| C、同位角相等 |
| D、一个锐角与一个钝角的和等于一个平角 |
已知：如图，矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AB=4cm，求矩形对角线的长和矩形面积．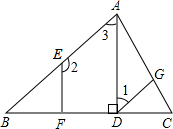
如图所示，已知AD⊥BC，垂足为点D，EF⊥BC，垂足为点F，∠1+∠2=180°．请填写∠CGD=∠CAB的理由．
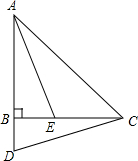如图，△ABC是等腰直角三角形，∠ABC=90°，D是AB延长线上一点，点E在BC边上，且BE=BD，连结AE，DC，∠BCD=15°，则∠AEC=
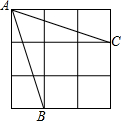如图是一个3×3的正方形网格，那么tan∠BAC=