题目内容
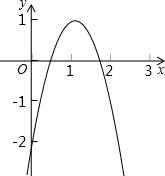
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴是直线x=1.①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述四个判断中正确的是
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴是直线x=1.①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述四个判断中正确的是考点:二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数与不等式(组)
专题:
分析:根据抛物线与x轴有两个交点可得b2-4ac>0,进而判断①正确;
根据题中条件不能得出x=-2时y的正负,因而不能得出②正确;
如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,由此判断③错误;
先根据抛物线的对称性可知x=-2与x=4时的函数值相等,再根据二次函数的增减性即可判断④正确.
根据题中条件不能得出x=-2时y的正负,因而不能得出②正确;
如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,由此判断③错误;
先根据抛物线的对称性可知x=-2与x=4时的函数值相等,再根据二次函数的增减性即可判断④正确.
解答:解:①∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,故①正确;
②x=-2时,y=4a-2b+c,而题中条件不能判断此时y的正负,即4a-2b+c可能大于0,可能等于0,也可能小于0,故②错误;
③如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,故③错误;
④∵二次函数y=ax2+bx+c的对称轴是直线x=1,
∴x=-2与x=4时的函数值相等,
∵4<5,
∴当抛物线开口向上时,在对称轴的右边,y随x的增大而增大,
∴y1<y2,故④正确.
故答案为:①④.
∴b2-4ac>0,
∴b2>4ac,故①正确;
②x=-2时,y=4a-2b+c,而题中条件不能判断此时y的正负,即4a-2b+c可能大于0,可能等于0,也可能小于0,故②错误;
③如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,故③错误;
④∵二次函数y=ax2+bx+c的对称轴是直线x=1,
∴x=-2与x=4时的函数值相等,
∵4<5,
∴当抛物线开口向上时,在对称轴的右边,y随x的增大而增大,
∴y1<y2,故④正确.
故答案为:①④.
点评:此题考查图象二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数的性质,以及二次函数与不等式的关系,根的判别式的熟练运用.

练习册系列答案
相关题目
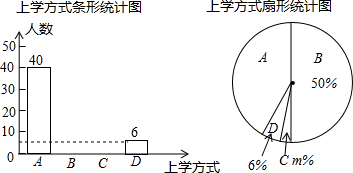
 如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )
如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )| A、1个 | B、2个 | C、3个 | D、4个 |
|-3|的绝对值是( )
| A、-3 | ||
B、-
| ||
| C、3 | ||
| D、±3 |
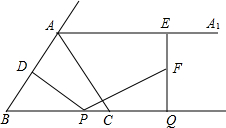 如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒.
如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒. 青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位) 如图,△ABC内接于⊙O,AB为⊙O的直径,且∠CAB=20°,则∠D的度数等于
如图,△ABC内接于⊙O,AB为⊙O的直径,且∠CAB=20°,则∠D的度数等于