题目内容
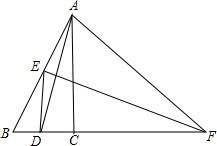 如图,已知AD是∠BAC的角平分线,AD的垂直平分线EF交AB于点E,交BC延长线于F.求证:
如图,已知AD是∠BAC的角平分线,AD的垂直平分线EF交AB于点E,交BC延长线于F.求证:(1)∠B=∠FAC;
(2)DE∥AC.
考点:线段垂直平分线的性质
专题:证明题
分析:(1)先根据线段垂直平分线的性质得出AF=DF,由等边对等角得到∠FAD=∠FDA,再根据角平分线定义得出∠BAD=∠CAD,从而利用三角形外角的性质及等式的性质即可证明∠B=∠FAC;
(2)先根据线段垂直平分线的性质得出AE=DE,由等边对等角得到∠ADE=∠EAD,而∠EAD=∠CAD,等量代换得出∠ADE=∠CAD,再根据内错角相等两直线平行即可证明DE∥AC.
(2)先根据线段垂直平分线的性质得出AE=DE,由等边对等角得到∠ADE=∠EAD,而∠EAD=∠CAD,等量代换得出∠ADE=∠CAD,再根据内错角相等两直线平行即可证明DE∥AC.
解答:证明:(1)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠FAC=∠B;
(2)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠ADE=∠EAD,
∵∠EAD=∠CAD,
∴∠ADE=∠CAD,
∴DE∥AC.
∴AF=DF,
∴∠FAD=∠FDA,
∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠FAC=∠B;
(2)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠ADE=∠EAD,
∵∠EAD=∠CAD,
∴∠ADE=∠CAD,
∴DE∥AC.
点评:本题考查了线段垂直平分线性质,三角形外角的性质,角平分线定义,平行线的判定等知识点的运用,难度适中,培养了学生综合运用性质进行推理的能力.

练习册系列答案
相关题目
线段AB被分为2:3:4三部分,已知第一部分和第三部分的中点间的距离是6.6cm,则线段AB的长为( )
| A、8.9cm |
| B、9.9cm |
| C、10.8cm |
| D、11.7cm |
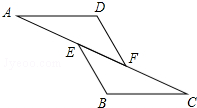 如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.
如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.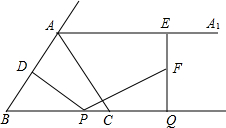 如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒.
如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒.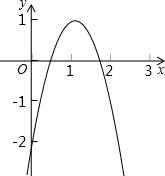 如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )
如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )