题目内容
11.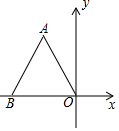 如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为(-2,-2$\sqrt{3}$).
如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为(-2,-2$\sqrt{3}$).
分析 过点A作AD⊥x轴于点D,根据等边三角形三线合一定理即可求出AD与OD的长度.
解答  解:过点A作AD⊥x轴于点D,
解:过点A作AD⊥x轴于点D,
由等边三角形的三线合一定理可知:OD=$\frac{1}{2}$OA=2,
由勾股定理可知:OA=$2\sqrt{3}$,
∴A(-2,-2$\sqrt{3}$)
故答案为:(-2,-2$\sqrt{3}$)
点评 本题考查等边三角形的性质,解题的关键是作出OB边上的高,然后利用三线合一定理求出AD与OD的长度,本题属于基础题型.

练习册系列答案
相关题目
2.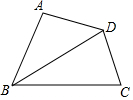 如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
 如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )| A. | 10 | B. | 12 | C. | 20 | D. | 无法确定 |
6.若5+$\sqrt{11}$与5-$\sqrt{11}$的整数部分分别为x,y,则x+y的立方根是( )
| A. | $\root{3}{9}$ | B. | ±$\root{3}{3}$ | C. | 3 | D. | ±$\root{3}{9}$ |
16.给出下列结论:
①任意两个等边三角形相似
②顶角对应相等的两个等腰三角形相似
③两条边对应成比例的两个直角三角形相似
其中正确的是( )
①任意两个等边三角形相似
②顶角对应相等的两个等腰三角形相似
③两条边对应成比例的两个直角三角形相似
其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
3.已知五边形ABCDE是⊙O的内接正五边形,则五边形ABCDE的中心角的度数为( )
| A. | 90° | B. | 72° | C. | 62° | D. | 60° |
 如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.
如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.