题目内容
12. 如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
分析 可设折痕对应的刻度为xcm,根据折叠的性质和三段长度由短到长的比为1:2:3,长为60cm的卷尺,列出方程求解即可.
解答 解:设折痕对应的刻度为xcm,依题意有
绳子被剪为10cm,20cm,30cm的三段,
①x=$\frac{20}{2}+10$=20,
②x=$\frac{30}{2}+10$=25
③x=$\frac{30}{2}+20$=35,
④x=$\frac{10}{2}+20$=25
⑤x=$\frac{10}{2}+30$=35
⑥x=$\frac{20}{2}+30$=40
综上所述,折痕对应的刻度可能为20、25、35,40;
故选:C.
点评 考查了一元一次方程的应用和图形的剪拼,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.注意分类思想的运用.

练习册系列答案
相关题目
2.某校男子足球队队员的年龄分布如表所示:
则这些队员年龄的中位数是15岁.
| 年龄(岁) | 13 | 14 | 15 | 16 | 17 |
| 人数 | 2 | 6 | 8 | 3 | 3 |
17.$\sqrt{64}$的立方根是( )
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
4.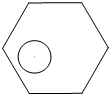 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )| A. | a2(2$\sqrt{3}$-aπ) | B. | r2(2π-$\sqrt{3}$) | C. | a2r2(2$\sqrt{3}$-π) | D. | r2(2$\sqrt{3}$-π) |
1.某班数学兴趣小组收集了本市4月份30天的日最高气温的数据,经过统计分析获得了两条信息和一个统计表(天数为正整数).
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
请根据上述信息求x,y,z的值.
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
| 气温℃ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 天数/天 | 2 | 3 | x | 5 | 4 | y | z | 3 | 2 | 3 |
2.甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲、乙所测得的成绩的平均数相同,且甲、乙成绩的方差分别为0.62、0.72,那么( )
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |