题目内容
4.解答下列各题:(1)已知$\frac{a}{b}$=$\frac{3}{2}$,且a+b=10,求a,b的值.
(2)计算:$\sqrt{12}$sin60°-6tan230°-2cos45°.
分析 (1)利用已知比例式表示出a,b的值,进而利用a+b=10求出答案;
(2)利用特殊角的三角函数值直接代入求出答案.
解答 解:(1)∵$\frac{a}{b}$=$\frac{3}{2}$,且a+b=10,
∴设a=3x,b=2x,则3x+2x=10,
解得:x=2,
故a=6,b=4;
(2)$\sqrt{12}$sin60°-6tan230°-2cos45°
=$\sqrt{12}$×$\frac{\sqrt{3}}{2}$-6×($\frac{\sqrt{3}}{3}$)2-2×$\frac{\sqrt{2}}{2}$
=3-6×$\frac{1}{3}$-$\sqrt{2}$
=1-$\sqrt{2}$.
点评 此题主要考查了特殊角的三角函数值以及比例式,正确记忆相关特殊角的三角函数值是解题关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
19. 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |

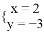 是二元一次方程4x+ay=7的一组解,则a的值为( )
是二元一次方程4x+ay=7的一组解,则a的值为( ) D.
D. 
 如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积. 如图,在△ABC中,∠A=90°,D为BC上一点,过D作ED⊥BC交AC于E,若AB=6,AC=8,ED=3,则CD的长为4.
如图,在△ABC中,∠A=90°,D为BC上一点,过D作ED⊥BC交AC于E,若AB=6,AC=8,ED=3,则CD的长为4. 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F.求证:EF=BE+CF.
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F.求证:EF=BE+CF.