题目内容
5.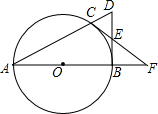 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.(1)求证:CF是⊙O的切线;
(2)若ED=3,cosF=$\frac{4}{5}$,求⊙O的半径.
分析 (1)连CB、OC,根据切线的性质得∠ABD=90°,根据圆周角定理由AB是直径得到∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,所以∠BCE=∠CBE,所以OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是⊙O的切线;
(2)CE=BE=DE=3,在Rt△BFE中,利用cosF=$\frac{BF}{EF}$=$\frac{4}{5}$,得出tanF=$\frac{BE}{BF}$=$\frac{3}{4}$,可计算出BF=4,再利用勾股定理可计算出EF=5,所以CF=CE+EF=8,然后在Rt△OCF中,利用正切定义可计算出OC.
解答 (1)证明:连CB、OC,如图,
∵BD为⊙O的切线,
∴DB⊥AB,
∴∠ABD=90°,
∵AB是直径,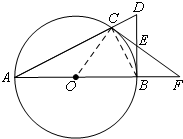
∴∠ACB=90°,
∴∠BCD=90°,
∵E为BD的中点,
∴CE=BE,
∴∠BCE=∠CBE,
而∠OCB=∠OBC,
∴∠OBC+∠CBE=∠OCB+∠BCE=90°,
∴OC⊥CF,
∴CF是⊙O的切线;
(2)解:CE=BE=DE=3,
在Rt△BFE中,cosF=$\frac{4}{5}$,tanF=$\frac{BE}{BF}$=$\frac{3}{4}$,
∴BF=4,
∴EF=$\sqrt{B{E}^{2}+B{E}^{2}}$=5,
∴CF=CE+EF=8,
在Rt△OCF中,tanF=$\frac{OC}{CF}$=$\frac{3}{4}$,
∴OC=6,
即⊙O的半径为6.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理、圆周角定理.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13.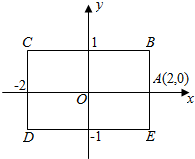 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )| A. | (-1,1) | B. | (-2,0) | C. | (-1,-1) | D. | (1,-1) |
10.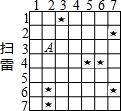 如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
 如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )| A. | (7,2) | B. | (2,6) | C. | (7,6) | D. | (4,5) |
15.若(x-2)(x+3)=x2+ax+b,则a、b的值分别为( )
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=1,b=6 | D. | a=5,b=-6 |
 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.