题目内容
20.计算:$\frac{1}{2}$×($\sqrt{3}$-1)2+$\frac{1}{\sqrt{2}}$+$\sqrt{12}$-($\frac{\sqrt{2}}{2}$)-1.分析 根据完全平方公式和负整数指数幂的意义得到原式=$\frac{1}{2}$×(3-2$\sqrt{3}$+1)+$\frac{\sqrt{2}}{2}$+2$\sqrt{3}$-$\sqrt{2}$,然后合并即可.
解答 解:原式=$\frac{1}{2}$×(3-2$\sqrt{3}$+1)+$\frac{\sqrt{2}}{2}$+2$\sqrt{3}$-$\sqrt{2}$
=2-$\sqrt{3}$+$\frac{\sqrt{2}}{2}$+2$\sqrt{3}$-$\sqrt{2}$
=2+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了负整数指数幂.

练习册系列答案
相关题目
5.比较$\sqrt{2}$和$\frac{\sqrt{5}}{2}$的大小( )
| A. | $\sqrt{2}$≥$\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$≤$\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$>$\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$<$\frac{\sqrt{5}}{2}$ |
10.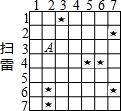 如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
 如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )| A. | (7,2) | B. | (2,6) | C. | (7,6) | D. | (4,5) |
 如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于C,交弦AB于D.求作此残片所在的圆(不写作法,保留作图痕迹).
如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于C,交弦AB于D.求作此残片所在的圆(不写作法,保留作图痕迹). 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.