题目内容
5.小明和小红一起做游戏,在一个不透明的袋中有8个白球和6个红球,它们除颜色外都相同,从袋中任意摸出一球,若摸到白球小明胜;若摸到红球小红胜,这个游戏公平吗?请说明理由;若你认为不公平,请你改动一下规则,使游戏对双方都是公平的.分析 根据概率公式可计算出P(小明胜)和P(小红胜),再比较两个概率的大小可判定游戏不公平,然后改动规则,满足袋中白球和红球的个数相等即可.
解答 解:不公平.
理由如下:∵P(小明胜)=$\frac{8}{8+6}$=$\frac{4}{7}$,P(小红胜)=$\frac{6}{8+6}$=$\frac{3}{7}$,
而$\frac{4}{7}$>$\frac{3}{7}$,
即P(小明胜)>P(小红胜),
∴这个游戏不公平;
可改为:从袋中取出2个白球或放入2个红球,使袋中白球和红球的个数相等,这样游戏对双方都是公平的.
点评 本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
10.若1<x<2,则化简|x-3|-$\sqrt{{x}^{2}-2x+1}$的结果为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
 如图,已知AB∥CD,∠ECD=∠EDC,求证:∠AEC=∠BED.
如图,已知AB∥CD,∠ECD=∠EDC,求证:∠AEC=∠BED.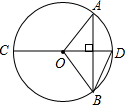 如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD=25°.
如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD=25°.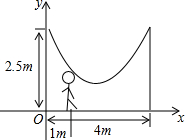 如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.