题目内容
已知一个多边形有两个内角是直角，其余的内角都等于150°，求这个多边形的边数．
考点：多边形内角与外角
专题：
分析：设这个多边形的边数为n，由于这个多边形有两个内角是直角，其余的内角都等于150°，所以这个多边形的内角和为90°×2+（n-2）×150°，又n边形的内角和为（n-2）×180°，根据此多边形的内角和不变列出方程，解方程即可．
解答：解：设这个多边形的边数为n，由题意得
90°×2+（n-2）×150°=（n-2）×180°，
解得n=8．
答：这个多边形的边数是8．
90°×2+（n-2）×150°=（n-2）×180°，
解得n=8．
答：这个多边形的边数是8．
点评：本题考查了多边形内角和定理：n边形的内角和为（n-2）×180°（n≥3且n为整数）．
练习册系列答案
相关题目
底角为30°，周长为40cm的等腰梯形，设中位线为xcm，当x为何值时，该梯形的面积最大？最大面积是多少？
如图是与“杨辉三角”有类似性质的数字三角形表，你能按照发现的规律把这个三角形继续写下去吗？和小伙伴比一比，看谁写得多．试试看．
如图，双曲线y=
如图，BE平分∠ABD，CF平分∠ACD，BE与CF相交于G，若∠BDC=140°，∠BGC=100°，求∠A的度数．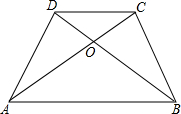
如图，在梯形ABCD中，CD=3，CO：OA=2：3，则AB=下列各式中，去括号正确的是（ ）
| A、a+（b-c+d）=a-b+c-d |
| B、a-（b-c+d）=a-b-c+d |
| C、a+（b-c+d）=a-b+c+d |
| D、a-（b-c+d）=a-b+c-d |