题目内容
学完“二次模式”这一章后，老师给茗茗布置了一道题，你帮帮茗茗做一下．
（1）根据以前学过的知识我们知道，两个有理数的积是1，则你这两个有理数互为倒数．同样，当两个实数a+
与a-
的积是1时，我们仍然称这两个实验数互为倒数．计算下列各式，并判断哪些式中的实数是互为倒数的．
①（2+
）（2-
）；
②（2+
）（2-
）；
③（3+2
）（3-2
）
④（4+
）（4-
）
⑤（5+
）（5-
）
（2）根据（1）中的计算和判断，请你用发现的规律，写出当实数a+
与a-
互为倒数时，a与b之间的数量关系；
（3）若x=8+3
，y=8-3
，则（xy）2003的值是多少？
（1）根据以前学过的知识我们知道，两个有理数的积是1，则你这两个有理数互为倒数．同样，当两个实数a+
| b |
| b |
①（2+
| 3 |
| 3 |
②（2+
| 5 |
| 5 |
③（3+2
| 2 |
| 2 |
④（4+
| 15 |
| 15 |
⑤（5+
| 26 |
| 26 |
（2）根据（1）中的计算和判断，请你用发现的规律，写出当实数a+
| b |
| b |
（3）若x=8+3
| 7 |
| 7 |
考点：分母有理化
专题：阅读型
分析：（1）先计算，再根据定义判定哪些式中的实数是互为倒数，
（2）由实数是互为倒数的定义求解即可，
（3）先求出xy，再求（xy）2003的值即可．
（2）由实数是互为倒数的定义求解即可，
（3）先求出xy，再求（xy）2003的值即可．
解答：解：（1）①（2+
）•（2-
）=1；
②（2+
）•（2-
）=-1；
③（3+2
）•（3-2
）=1；
④（4+
）•（4-
）=1；
⑤（5+
）•（5-
）=-1；
所以①③④中的实数是互为倒数的．
（2）由（a+
）•（a-
）=a2-b，
可得a2-b=1时，实数a+
与a-
互为倒数．
（3）∵x=8+3
，y=8-3
，
∴xy=1
∴（xy）2003=1．
| 3 |
| 3 |
②（2+
| 5 |
| 5 |
③（3+2
| 2 |
| 2 |
④（4+
| 15 |
| 15 |
⑤（5+
| 26 |
| 26 |
所以①③④中的实数是互为倒数的．
（2）由（a+
| b |
| b |
可得a2-b=1时，实数a+
| b |
| b |
（3）∵x=8+3
| 7 |
| 7 |
∴xy=1
∴（xy）2003=1．
点评：本题主要考查了分母有理化，解题的关键是理解题中的概念．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图，在△PAB中，点C、D在边AB上，PC=PD=CD，∠APB=120°．
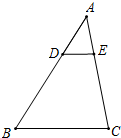在△ABC中，D和E分别在AB、AC上，且DE∥BC，AD：DB=1：2，则下列结论中正确的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的一元二次方程mx2-2x+1=0有实数根，则实数m的取值范围是（ ）
| A、m≥1 |
| B、m≤1 |
| C、m≥1且m≠0 |
| D、m≤1且m≠0 |