题目内容
 如图,BE平分∠ABD,CF平分∠ACD,BE与CF相交于G,若∠BDC=140°,∠BGC=100°,求∠A的度数.
如图,BE平分∠ABD,CF平分∠ACD,BE与CF相交于G,若∠BDC=140°,∠BGC=100°,求∠A的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:连接BC,根据三角形内角和定理求出∠DBC+∠DCB=40°,∠GBC+∠GCB=80°,所以∠GBD+∠GCD=40°,再根据角平分线的定义求出∠ABG+∠ACG=40°,然后根据三角形内角和定理即可求出∠A=60°.
解答: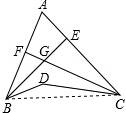 解:连接BC,
解:连接BC,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∵∠BGC=100°,
∴∠GBC+∠GCB=180°-100°=80°,
∴∠GBD+∠GCD=80°-40°=40°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=40°,
在△ABC中,∠A=180°-40°-40°-40°=60°.
故∠A的度数为60°.
 解:连接BC,
解:连接BC,∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∵∠BGC=100°,
∴∠GBC+∠GCB=180°-100°=80°,
∴∠GBD+∠GCD=80°-40°=40°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=40°,
在△ABC中,∠A=180°-40°-40°-40°=60°.
故∠A的度数为60°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若A、B、C在同一直线上,AB=3cm,BC=5cm,则AC的长为( )
| A、2cm |
| B、8cm |
| C、2cm或8cm |
| D、4cm或8cm |
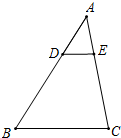 在△ABC中,D和E分别在AB、AC上,且DE∥BC,AD:DB=1:2,则下列结论中正确的是( )
在△ABC中,D和E分别在AB、AC上,且DE∥BC,AD:DB=1:2,则下列结论中正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,四边形ABCD的四个顶点都在⊙O上,AC是直径,DE⊥AC,垂足为点E,DE与CB的延长线相交于点F,求证:CD2=CB•CF.
如图,四边形ABCD的四个顶点都在⊙O上,AC是直径,DE⊥AC,垂足为点E,DE与CB的延长线相交于点F,求证:CD2=CB•CF.