题目内容
20.已知:x2-5xy+4y2=0,且xy≠0,则x:y=( )| A. | 1或4 | B. | 1或$\frac{1}{4}$ | C. | -1或-4 | D. | -1或-$\frac{1}{4}$ |
分析 已知等式左边利用十字相乘法分解因式后,利用两项相乘积为0两因式中至少有一个为0求出x与y的比值即可.
解答 解:已知等式分解得:(x-4y)(x-y)=0,
可得x-4y=0或x-y=0,
解得:x=4y或x=y,
则x:y=4或1.
故选A
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘的方法是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
10.有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则只有1人不能上车,下列四个方程错误的是( )
| A. | 40m-10=43m-1 | B. | 40m+10=43m+1 | C. | 43(n-10)=40(n-1) | D. | $\frac{n-10}{40}$=$\frac{n-1}{43}$ |
 如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).
如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).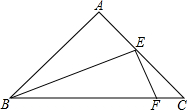 如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.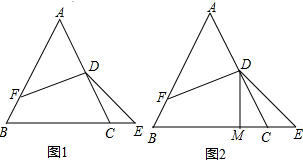
 已知:如图,四边形ABCD中,∠A=∠C=90°,∠D=60°,AD=5$\sqrt{3}$,AB=3,求BC的长.
已知:如图,四边形ABCD中,∠A=∠C=90°,∠D=60°,AD=5$\sqrt{3}$,AB=3,求BC的长.