题目内容
10. 如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )
如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )| A. | 8米 | B. | 7米 | C. | 5米 | D. | 5$\sqrt{3}$米 |
分析 先构建直角三角形,再利用勾股定理和垂径定理计算.
解答  解:因为跨度AB=24m,拱所在圆半径为13m,
解:因为跨度AB=24m,拱所在圆半径为13m,
延长CD到O,使得OC=OA,则O为圆心,
则AD=$\frac{1}{2}$AB=12(米),
则OA=13米,
在Rt△AOD中,DO=$\sqrt{O{A}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5(米),
进而得拱高CD=CO-DO=13-5=8米.
故选:A.
点评 本题主要考查了垂径定理的应用、勾股定理;根据题意作出辅助线构造直角三角形是解答此题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.若用a、b表示2+$\sqrt{5}$的整数部分和小数部分,则a、b可表示为( )
| A. | 4和$\sqrt{5}$-2 | B. | 3和$\sqrt{5}$-3 | C. | 2和$\sqrt{5}$-2 | D. | 5和$\sqrt{5}$-5 |
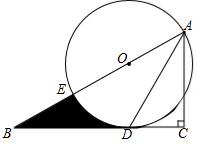 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,圆心在AB上,以AD为弦的⊙O交AB于点E.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,圆心在AB上,以AD为弦的⊙O交AB于点E.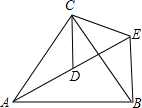 如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.