题目内容
20.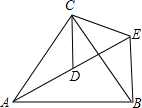 如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.(1)求证:△ACD≌△BCE;
(2)若CE=16,BE=21,求AE的长.
分析 (1)根据等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,根据全等三角形的判定得出即可;
(2)根据全等得出AD=BE=21,求出DE=CE=16,即可得出答案.
解答 (1)证明:∵△ACB和△ECD都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(2)∵△ACD≌△BCE,
∴AD=BE=21,
∵△ECD是等边三角形,
∴DE=CE=16,
∴AE=AD+DE=21+16=37.
点评 本题考查了等边三角形的性质,全等三角形的性质和判定的应用,能推出△ACD≌△BCE是解此题的关键.

练习册系列答案
相关题目
10. 如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )
如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )
 如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )
如图,一座石拱桥是圆弧形,其跨度(AB长)为24米,半径为13米,则拱高(CD长)为( )| A. | 8米 | B. | 7米 | C. | 5米 | D. | 5$\sqrt{3}$米 |
5. 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
 如图,C为线段AB上一动点(不与点A、B重合),在AB同侧分别作正三角形ACD和正三角形BCE,AE与BD交于点F,AE与CD交于点G,BD与CE交于点H,连接GH.以下五个结论:①AE=BD;②GH∥AB;③AD=DH;④GE=HB;⑤∠AFD=60°,一定成立的是( )
如图,C为线段AB上一动点(不与点A、B重合),在AB同侧分别作正三角形ACD和正三角形BCE,AE与BD交于点F,AE与CD交于点G,BD与CE交于点H,连接GH.以下五个结论:①AE=BD;②GH∥AB;③AD=DH;④GE=HB;⑤∠AFD=60°,一定成立的是( )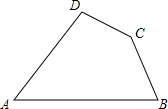 根据下列语句画出图形:
根据下列语句画出图形: