题目内容
12.关于x的方程(k-1)x2+2kx+2=0(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=x1x2-x1-x2,S的值能为1吗?若能,求出此时k的值;若不能,请说明理由.
分析 (1)分二次项系数为0和非0两种情况考虑,当k-1=0时,原方程为一元一次方程,解方程可得出此时方程有实数根;当k-1≠0时,根据根的判别式△=b2-4ac,可得出△=4(k-1)2+4>0,进而可得出方程有两个不相等的实数根,综上即可得出结论.
(2)假设能,根据根与系数的关系可得出${x_1}+{x_2}=\frac{-2k}{k-1}$、${x_1}{x_2}=\frac{2}{k-1}$,将S进行变形代入数据即可得出分式方程$\frac{2}{k-1}+\frac{2k}{k-1}=1$,解分式方程得出k值,经检验后即可得出结论.
解答 (1)证明:①当k-1=0即k=1时,方程为一元一次方程2x=2,
x=1有一个解;
②当k-1≠0即k≠1时,方程为一元二次方程,
∵△=(2k)2-4×2(k-1)=4k2-8k+8=4(k-1)2+4>0,
∴方程有两个不相等的实数根.
综合①②得:不论k为何值,方程总有实根.
(2)解:假设能,∵x1,x2是方程(k-1)x2+2kx+2=0的两个根,
∴${x_1}+{x_2}=\frac{-2k}{k-1}$,${x_1}{x_2}=\frac{2}{k-1}$,
∴S=x1x2-x1-x2=x1x2-(x1+x2)=1,即$\frac{2}{k-1}+\frac{2k}{k-1}=1$,
整理得:2+2k=k-1,解得:k=-3.
经检验:k=-3是分式方程$\frac{2}{k-1}+\frac{2k}{k-1}=1$的解.
∴S的值能为1,此时k的值为-3.
点评 本题考查了根与系数的关系、根的判别式以及解分式方程,熟练掌握根与系数的关系以及根的判别式是解题的关键.

练习册系列答案
相关题目
20.甲、乙两名队员参加射击训练,成绩分别被制成如图两个统计图:
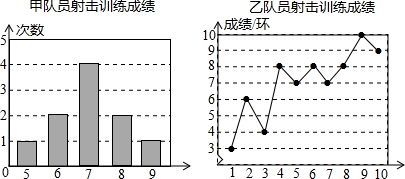
根据以上信息,整理分析数据如表:
(1)写出表格中a,b,c的值:a=7,b=7.5,c=1.2;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如表:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | c |
| 乙 | 7 | b | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
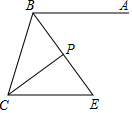 已知:如图AB∥CE,BE平分∠ABC,CP平分∠BCE交BE于点P.
已知:如图AB∥CE,BE平分∠ABC,CP平分∠BCE交BE于点P.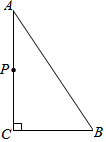 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
 如图所示,在△ABC中,∠C=90°,它的内切⊙O分别与边AB,BC,CA相切于点D,E,F,且BD=12,半径r=4,求AD的长.
如图所示,在△ABC中,∠C=90°,它的内切⊙O分别与边AB,BC,CA相切于点D,E,F,且BD=12,半径r=4,求AD的长. 如图,在△ABC中,点D是边BC上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠DAC的度数.
如图,在△ABC中,点D是边BC上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠DAC的度数.