题目内容
11. 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 5 | B. | 13 | C. | 6.5 | D. | $\frac{60}{13}$ |
分析 根据菱形的性质:对角线互相垂直,利用勾股定理求出AD,再利用直角三角形斜边的中线的性质OE=$\frac{1}{2}$AD,求出OE即可.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=$\frac{1}{2}$AC=5,OD=$\frac{1}{2}$BD=12,
在Rt△AOD中,AD=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵AE=DE,
∴OE=$\frac{1}{2}$AD=6.5
故选C.
点评 此题主要考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半等知识,得出EO=$\frac{1}{2}$AD是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
2.如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为-5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为$\frac{1}{3}$BC的点N,则该数轴的原点为( )
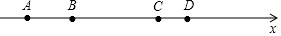
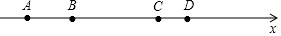
| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
19. 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
其中,b=2;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | b | 1 | 0 | 1 | 2 | … |
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
3.若a<0,则下列不等式不成立的是( )
| A. | a+2<a+3 | B. | 2a<3a | C. | 2-a<3-a | D. | $\frac{a}{2}$<$\frac{a}{3}$ |
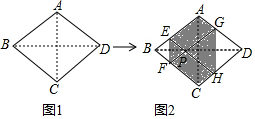 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: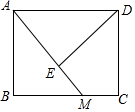 如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为$\frac{2\sqrt{5}}{5}$.
如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为$\frac{2\sqrt{5}}{5}$.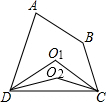 如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.
如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.