题目内容
20.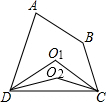 如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.
如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.
分析 先根据∠ADC、∠BCD的平分线交于点O1,得出∠O1DC+∠O1CD=$\frac{1}{2}$(∠ADC+∠DCB),再根据∠O1DC、∠O1CD的平分线交于点O2,得出∠O2DC+∠O2CD=$\frac{1}{{2}^{2}}$(∠ADC+∠DCB),根据规律可得到∠O5DC+∠O5CD=$\frac{1}{{2}^{5}}$(∠ADC+∠DCB),最后将∠ADC+∠DCB=160°代入计算即可.
解答  解:如图所示,∵∠ADC、∠BCD的平分线交于点O1,
解:如图所示,∵∠ADC、∠BCD的平分线交于点O1,
∴∠O1DC+∠O1CD=$\frac{1}{2}$(∠ADC+∠DCB),
∵∠O1DC、∠O1CD的平分线交于点O2,
∴∠O2DC+∠O2CD=$\frac{1}{2}$(∠O1DC+∠O1CD)=$\frac{1}{{2}^{2}}$(∠ADC+∠DCB),
同理可得,∠O3DC+∠O3CD=$\frac{1}{2}$(∠O2DC+∠O2CD)=$\frac{1}{{2}^{3}}$(∠ADC+∠DCB),
由此可得,∠O5DC+∠O5CD=$\frac{1}{2}$(∠O4DC+∠O4CD)=$\frac{1}{{2}^{5}}$(∠ADC+∠DCB),
∴△CO5D中,∠CO5D=180°-(∠O5DC+∠O5CD)=180°-$\frac{1}{{2}^{5}}$(∠ADC+∠DCB),
又∵四边形ABCD中,∠DAB+∠ABC=200°,
∴∠ADC+∠DCB=160°,
∴∠CO5D=180°-$\frac{1}{{2}^{5}}$×160°=180°-5°=175°,
故答案为:175°.
点评 本题主要考查了多边形的内角与外角以及角平分线的定义的运用,解决问题的关键是找出操作的变化规律,得到∠CO5D与∠ADC+∠DCB之间的关系.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案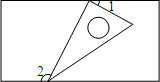 如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 5 | B. | 13 | C. | 6.5 | D. | $\frac{60}{13}$ |
 已知一次函数y=kx+b的图象如图所示,当x>3时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x>3时,y的取值范围是( )| A. | y>3 | B. | y<0 | C. | 0<y<3 | D. | y<3 |
| A. | x-1<y-1 | B. | 3x<3y | C. | $\frac{x}{2}$<$\frac{y}{2}$ | D. | -2x<-2y |
| A. | (x-3)2=11 | B. | (x-3)2=7 | C. | (x+3)2=7 | D. | (x-3)2=2 |
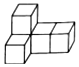 有5个大小相同的小正方体,它们的棱长为1,将这5个正方体拼成如图所示的几何体,则下列说法正确的是( )
有5个大小相同的小正方体,它们的棱长为1,将这5个正方体拼成如图所示的几何体,则下列说法正确的是( )| A. | 主视图的面积为3 | B. | 左视图的面积为3 | ||
| C. | 俯视图的面积为5 | D. | 三个视图的面积相等 |
 如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是1.
如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是1.