题目内容
2.如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为-5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为$\frac{1}{3}$BC的点N,则该数轴的原点为( )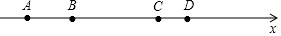
| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
分析 根据A、D两点在数轴上所表示的数,求得AD的长度,然后根据2AB=BC=3CD,求得AB、BC,CD的长度,从而找到E,M,N所表示的数.
解答  解:如图所示:
解:如图所示:
∵2AB=BC=3CD,
∴设CD=x,则BC=3x,AB=1.5x,
∵A、D两点表示的数分别为-5和6,
∴x+3x+1.5x=11,
解得:x=2,
故CD=2,BC=6,AB=3,
∵AC的中点为E,BD的中点为M,
∴AE=EC=4.5,BM=MD=4,
则E点对应的数字是-0.5,M对应的数字为:2,
∵BC之间距点B的距离为$\frac{1}{3}$BC的点N,
∴BN=$\frac{1}{3}$BC=2,
故AN=5,则N正好是原点.
故选:D.
点评 本题考查了数轴、比较线段的长短.灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
相关题目
13.一组数据5,1,x,6,4的众数是4,这组数据的方差是( )
| A. | $\sqrt{2}$ | B. | 2.8 | C. | 2 | D. | $\sqrt{10}$ |
10.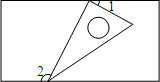 如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
 如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=20°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
17.下列运算正确的是( )
| A. | (-a)4=a4 | B. | 8a-a=8 | C. | a3×a2=a6 | D. | (a-b)2=a2-b2 |
7.下列所述的图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 平行四边形 | B. | 等腰直角三角形 | C. | 菱形 | D. | 正五边形 |
11. 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )
 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=10,BD=24,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 5 | B. | 13 | C. | 6.5 | D. | $\frac{60}{13}$ |
12.用配方法解方程x2-6x+2=0,原方程可变形为( )
| A. | (x-3)2=11 | B. | (x-3)2=7 | C. | (x+3)2=7 | D. | (x-3)2=2 |
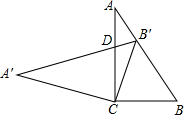 在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.
在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.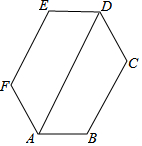 如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )