题目内容
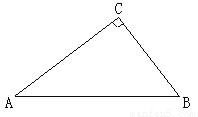
如图,在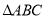 中,
中, 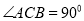 ,点
,点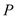 到
到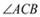 两边的距离相等,且
两边的距离相等,且 .
.
(1)先用尺规作出符合要求的点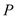 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设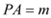 ,
,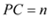 ,试用
,试用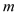 、
、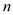 的代数式表示
的代数式表示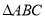 的周长和面积;
的周长和面积;
(3)设 与
与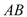 交于点
交于点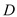 ,试探索当边
,试探索当边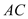 、
、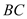 的长度变化时,
的长度变化时,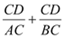 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
【答案】(1)作图见解析;ΔABP是等腰直角三角形. 理由见解析;(2)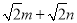 ;
; 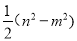 (3)
(3)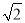 .
.
【解析】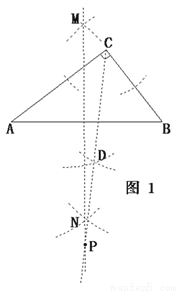 (1)依题意,点P既在
(1)依题意,点P既在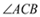 的平分线上,
的平分线上,
又在线段AB的垂直平分线上.
如图1,作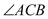 的平分线
的平分线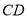 ,
,
作线段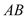 的垂直平分线
的垂直平分线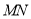 ,
, 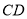 与
与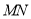 的
的
交点即为所求的P点。┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分
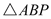 是等腰直角三角形.
是等腰直角三角形.
理由:过点P分别作 、
、 ,垂足为E、F如图2.
,垂足为E、F如图2.
∵ 平分
平分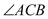 ,
, 、
、 ,垂足为E、F,
,垂足为E、F,
∴ .
.
又∵  ,∴
,∴  ≌
≌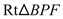 .┄┄┄┄┄┄┄┄4分
.┄┄┄┄┄┄┄┄4分
∴  .
.
∵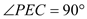 ,
,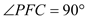 ,
, ,
,
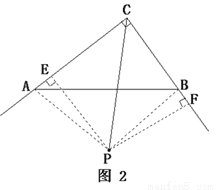 ∴
∴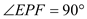 , 从而
, 从而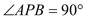 .
.
又 ∴
∴  是等腰直角三角形. ┄┄┄┄┄┄┄┄5分
是等腰直角三角形. ┄┄┄┄┄┄┄┄5分
(2)如图2,在 中,
中,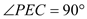 ,
,
 ,
,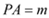 . ∴
. ∴ .
.
由 ≌
≌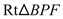 ,
,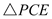 ≌
≌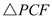 ,
,
可得 ,
, .
.
∴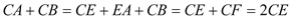 .
.
在 中,
中,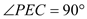 ,
,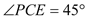 ,
, ,
,
∴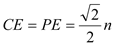 . ∴
. ∴ . ┄┄┄┄6分
. ┄┄┄┄6分
所以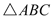 的周长为:
的周长为: . ┄┄┄┄7分
. ┄┄┄┄7分
因为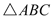 的面积=
的面积=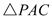 的面积
的面积
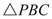 的面积
的面积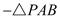 的面积
的面积
=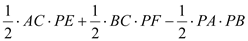 =
=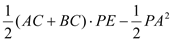
=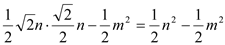 (
(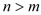 )┄┄9分
)┄┄9分
或 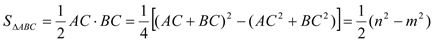 .
.
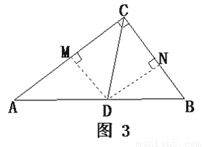
(3)过点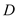 分别作
分别作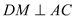 、
、 ,垂足为
,垂足为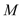 、
、 如图3.
如图3.
 ∵
∵ 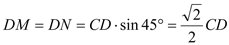 .┄┄┄┄10分
.┄┄┄┄10分
由 ∥
∥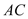 得
得 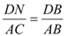 ①┄┄┄┄┄┄┄┄11分
①┄┄┄┄┄┄┄┄11分
由 ∥
∥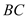 得
得 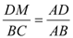 ② ┄┄┄┄┄┄12分
② ┄┄┄┄┄┄12分
①+②,得 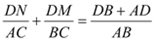 ,即
,即 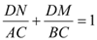 .
.
∴ 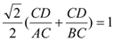 , 即
, 即 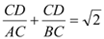 ┄┄┄┄13分
┄┄┄┄13分
【点睛】(1)由题意作出∠ACB的角平分线和线段AB的垂直平分线可求出点P,然后证明Rt△APE≌Rt△BPF即可;
(2)由PA=PB,PA=m,可得出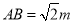 ,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知
,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知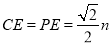 ,即
,即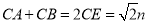 ,最后求出周长和面积;
,最后求出周长和面积;
(3)由平行线分线段成比例定理得到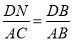 ,
, 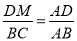 是解答本题的关键.
是解答本题的关键.
【题型】解答题
【结束】
15
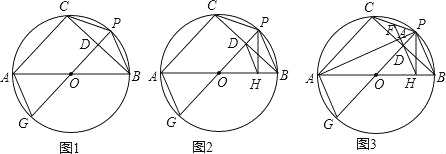
⊙O是△ABC的外接圆,AB是直径,过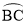 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2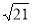 ,求AC的长.
,求AC的长.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案

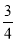 .
.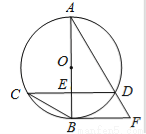
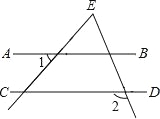
 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.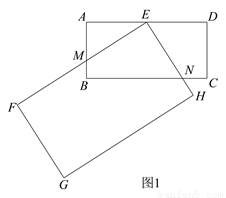

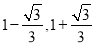 .
.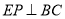 ,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN=
,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN= 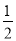 PC,进而求出PN=CN=
PC,进而求出PN=CN=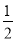 ,再判断出AM=PN=
,再判断出AM=PN=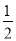 ,即可得出BM=
,即可得出BM=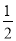 ,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.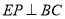 ,垂足为点 P,
,垂足为点 P,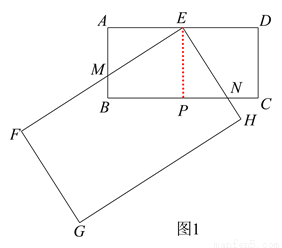
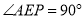 ,
,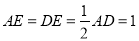 ,∴PE=AE,
,∴PE=AE,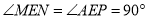 ,∴
,∴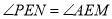 ,
,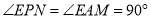 ,∴
,∴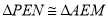 ,∴EM=EN.
,∴EM=EN.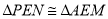 ,∴AM=PN,
,∴AM=PN,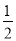 PC,
PC,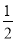 ,
,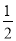 ,BM=AB-AM=
,BM=AB-AM=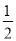 ,∴AM=BN.
,∴AM=BN.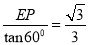 ,
,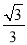 ,CM=PC+PM=1+
,CM=PC+PM=1+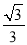 ,
,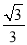 ,1+
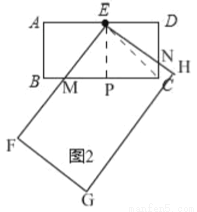
,1+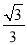 .
.
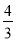 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.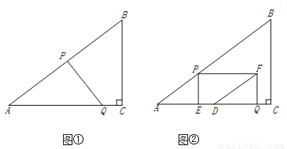
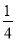 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的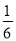 ,求道路的宽.
,求道路的宽.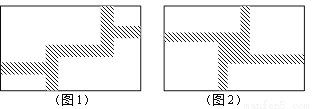
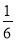 ,列方程求解即可.
,列方程求解即可.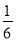 ×20×12,
×20×12,