题目内容
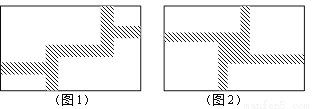
(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的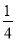 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的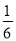 ,求道路的宽.
,求道路的宽.
【答案】(1)道路宽为2米;(2)道路的宽为1米.
【解析】试题分析:(1)设道路宽为x米,利用平移把不规则的图形变为规则图形,如此一来,所有草坪面积之和就变为了(20﹣x)(12﹣x)米2,进而即可列出方程,求出答案;
(2)设道路的宽为x米,则正方形边长为4x,根据道路与观赏亭的面积之和是矩形面积的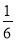 ,列方程求解即可.
,列方程求解即可.
试题解析:【解析】
(1)设道路宽为x米,
根据题意得:(20﹣x)(12﹣x)=180
解得:x1=30(舍去),x2=2
答:道路宽为2米;
(2)设道路的宽为x米,
则可列方程:x(12-4x)+x(20-4x)+16x2=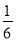 ×20×12,
×20×12,
即:x2+4x-5=0,
解得:x1=1,x2=-5(舍去),
答:道路的宽为1米.
点睛:考查了一元二次方程的应用,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.另外还要注意解的合理性,从而确定取舍.
【题型】解答题
【结束】
10
如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.

(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
(1)作图见解析;(2)∠ABM=30°. 【解析】分析:(1)将图4中的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图中的平行四边形,此平行四边形即为图2中的四边形ABCD. (2)根据题意先求得AB=30cm,由纸带的宽为15cm,根据三角函数求得∠AMB=30°. 本题解析:(1)如图: (2)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=3... 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案

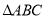 中,
中,  ,点
,点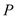 到
到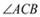 两边的距离相等,且
两边的距离相等,且 .
.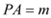 ,
,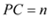 ,试用
,试用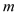 、
、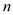 的代数式表示
的代数式表示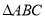 的周长和面积;
的周长和面积; 与
与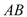 交于点
交于点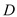 ,试探索当边
,试探索当边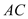 、
、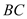 的长度变化时,
的长度变化时,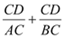 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.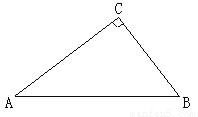
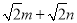 ;
; 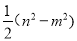 (3)
(3)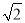 .
.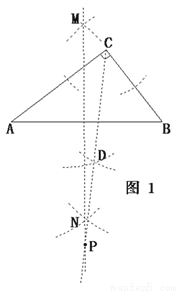 (1)依题意,点P既在
(1)依题意,点P既在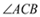 的平分线上,
的平分线上,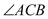 的平分线
的平分线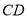 ,
,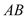 的垂直平分线
的垂直平分线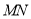 ,
, 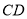 与
与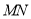 的
的 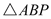 是等腰直角三角形.
是等腰直角三角形.  、
、 ,垂足为E、F如图2.
,垂足为E、F如图2. 平分
平分 .
. ,∴
,∴  ≌
≌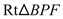 .┄┄┄┄┄┄┄┄4分
.┄┄┄┄┄┄┄┄4分 .
. 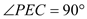 ,
,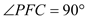 ,
, ,
,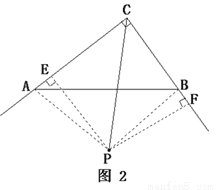 ∴
∴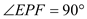 , 从而
, 从而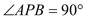 .
.  中,
中,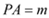 . ∴
. ∴ .
. 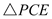 ≌
≌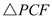 ,
, ,
, .
.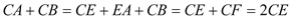 .
.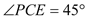 ,
, ,
,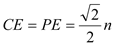 . ∴
. ∴ . ┄┄┄┄6分
. ┄┄┄┄6分  的周长为:
的周长为: . ┄┄┄┄7分
. ┄┄┄┄7分 的面积
的面积
 的面积
的面积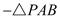 的面积
的面积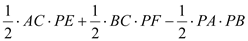 =
=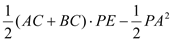
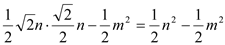 (
(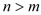 )┄┄9分
)┄┄9分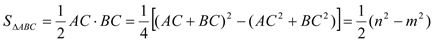 .
. 分别作
分别作 、
、 ,垂足为
,垂足为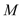 、
、 如图3.
如图3.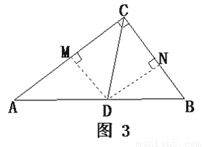 ∵
∵ 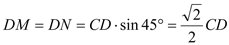 .┄┄┄┄10分
.┄┄┄┄10分  ∥
∥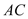 得
得 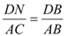 ①┄┄┄┄┄┄┄┄11分
①┄┄┄┄┄┄┄┄11分 ∥
∥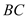 得
得 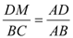 ② ┄┄┄┄┄┄12分
② ┄┄┄┄┄┄12分 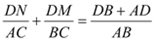 ,即
,即 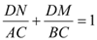 .
. 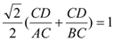 , 即
, 即 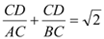 ┄┄┄┄13分
┄┄┄┄13分 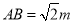 ,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知
,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知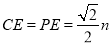 ,即
,即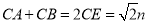 ,最后求出周长和面积;
,最后求出周长和面积;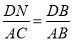 ,
, 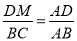 是解答本题的关键.
是解答本题的关键.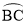 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.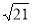 ,求AC的长.
,求AC的长.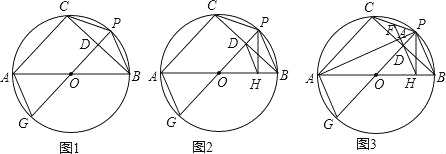
 的值.
的值.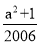 =
= .
.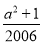 =-a-1+
=-a-1+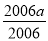 =-1,即a2-2007a+
=-1,即a2-2007a+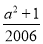 =-1.
=-1.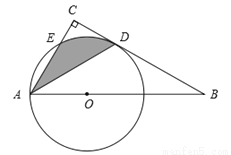
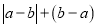 的结果为( )
的结果为( )
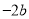 C.
C. 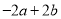 D.
D. 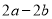
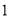 个过滤网要花费
个过滤网要花费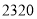 元,买
元,买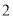 个空气净化器和
个空气净化器和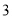 个过滤网要花费
个过滤网要花费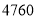 元.
元.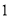 )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?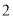 )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买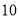 个空气净化器和
个空气净化器和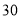 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.