题目内容
10.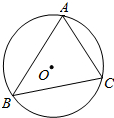 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于4$\sqrt{3}$.
如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于4$\sqrt{3}$.
分析 连接OA,OC,过点O作OD⊥AC于点D,由圆周角定理求出∠AOC的度数,再由垂径定理得出AD=$\frac{1}{2}$AC,∠AOD=$\frac{1}{2}$∠AOC,根据锐角三角函数的定义求出AD的长,进而可得出结论.
解答 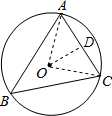 解:连接OA,OC,过点O作OD⊥AC于点D,
解:连接OA,OC,过点O作OD⊥AC于点D,
∵∠B=60°,
∴∠AOC=120°.
∵OD⊥AC,OA=4,
∴AD=$\frac{1}{2}$AC,∠AOD=$\frac{1}{2}$∠AOC=60°,
∴AD=OA•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AC=2AD=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是圆周角定理,根据题意作出辅助线,利用垂径定理及直角三角形的性质求解是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
2.下列判断正确的是( )
| A. | $-\frac{3}{5}$<$-\frac{4}{7}$ | B. | x-2是有理数,它的倒数是$\frac{1}{x-2}$ | ||
| C. | 若|a|=|b|,则a=b | D. | 若|a|=-a,则a<0 |
3.以3和4为根的一元二次方程是( )
| A. | x2-7x+12=0 | B. | x2+7x+12=0 | C. | x2+7x-12=0 | D. | x2-7x-12=0 |
 如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3).
如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3). 如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.
如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.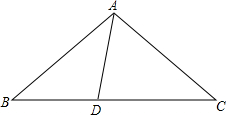 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,∠ADB=100°,则∠BAC的度数为100°.
如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,∠ADB=100°,则∠BAC的度数为100°.