题目内容
20. 如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3).
如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3).(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为$\frac{3\sqrt{3}}{2}$,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
分析 (1)通过求函数解析式,求出相应线段的长度,观察AC=2OA,进而求出∠ABC度数;
(2)通过观察三角形ADC面积与三角形AOC面积相等,可以判断直线OD∥AC,求出直线与抛物线交点即为点D;
(3)利用抛物线解析式设出O′,通过旋转60°,求出点B′的坐标,将点B′代入抛物线解析式即可求出.
解答 解:(1)由题意与y轴交于点C(0,-3),
∴得解析式为y=x2-3,
令y=0,x=±$\sqrt{3}$,
∴B($\sqrt{3}$,0),A(-$\sqrt{3}$,0),
∴OA=$\sqrt{3}$,OC=3,AC=2$\sqrt{3}$,
∴∠OCA=30°,
∴∠ABC=60°;
(2)由(1)得:OA=$\sqrt{3}$,OC=3,
∴S△OAC=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
过原点与AC平行的直线y=-$\sqrt{3x}$,
直线与抛物线的交点即为点D,
联立:$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{y={x}^{2}-3}\end{array}\right.$,
解得x1=$\frac{-\sqrt{3}+\sqrt{15}}{2}$,x2=$\frac{-\sqrt{3}-\sqrt{15}}{2}$(舍去),
∴D ($\frac{-\sqrt{3}+\sqrt{15}}{2}$,$\frac{3-3\sqrt{5}}{2}$).
(3)设点O′(m,m2-3),
∵顺时针旋转60°,
则点B′(m+$\frac{\sqrt{3}}{2}$,m2-$\frac{9}{2}$),
∴(m+$\frac{\sqrt{3}}{2}$)2-3=m2-$\frac{9}{2}$,
∴m=-$\frac{3\sqrt{3}}{4}$,
∴O′(-$\frac{3\sqrt{3}}{4}$,-$\frac{21}{16}$).
点评 题目考查二次函数综合应用,涉及二次函数解析式、三角形面积,一次函数解析式确定及旋转,题目整体较难,适合学生中考压轴题的拔高训练.

 如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )| A. | 两点之间,线段最短 | B. | 两点确定一条直线 | ||
| C. | 两点之间,直线最短 | D. | 两点确定一条线段 |
 在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.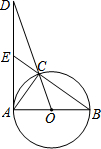 如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.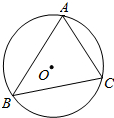 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于4$\sqrt{3}$.
如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于4$\sqrt{3}$.