题目内容
19．先化简，再求值：（$\frac{{x}^{2}-2x+4}{x-1}$-x+2）÷$\frac{{x}^{2}+4x+4}{1-x}$，其中x=$\sqrt{3}$-2．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{{x}^{2}-2x+4-（x-1）（x-2）}{x-1}$•$\frac{-（x-1）}{（x+2）^{2}}$=-$\frac{x+2}{x-1}$•$\frac{x-1}{（x+2）^{2}}$=-$\frac{1}{x+2}$，
当x=$\sqrt{3}$-2时，原式=-$\frac{\sqrt{3}}{3}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
9．将一张大小为10cm×10cm的正方形纸片，依下图所示方式折叠并剪裁后再展开，其中折线（虚线）正好过三角形两边的中点，则展开后内部的正方形（无阴影部分）面积等于（ ）
| A． | 25cm2 | B． | 50cm2 | C． | 75cm2 | D． | 40cm |
10．
如图，已知DE为三角形ABC的中位线，且AB=8，AC=7，BC=6，则三角形ADE的周长（ ）
如图，已知DE为三角形ABC的中位线，且AB=8，AC=7，BC=6，则三角形ADE的周长（ ）| A． | 21 | B． | 10.5 | C． | 18 | D． | 17 |
如图，在平行四边形ABCD中，AB=3，AD=4，∠ABC=60°，过BC的中点E作EF⊥AB于点F，交DC的延长线于点G，则DE=$\sqrt{19}$．
11．
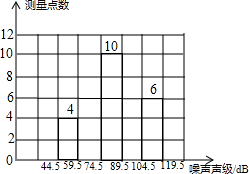为了增强环境保护意识，在“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，随机抽查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将抽查得到的数据进行整理（设所测数据是正整数），得频数分布表如表：
根据表中提供的信息解答下列问题：
（1）频数分布表中的a=8，b=12，c=0.3；
（2）补充完整频数分布直方图；
（3）如果全市共有400个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
为了增强环境保护意识，在“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，随机抽查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将抽查得到的数据进行整理（设所测数据是正整数），得频数分布表如表：| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5-59.5 | 4 | 0.1 |
| 2 | 59.5-74.5 | a | 0.2 |
| 3 | 74.5-89.5 | 10 | 0.25 |
| 4 | 89.5-104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
（1）频数分布表中的a=8，b=12，c=0.3；
（2）补充完整频数分布直方图；
（3）如果全市共有400个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
8．
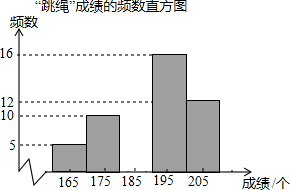某校为了解九年级学生的身体素质情况，从全校500名九年级学生中随机抽取了部分学生进行体育测试，其中“跳绳”成绩制成如下频数表和频数直方图：
“跳绳”成绩的频数表
根据图表解决下列问题：
（1）本次抽样调查的样本容量是50，频数表中，a=0.2，b=7c=0.32；
（2）数据分组的组距是10，本次调查的个体是被抽到的每名九年级学生的跳绳成绩；
（3）补全频数直方图；
（4）“跳绳”数在180以上，则此项成绩可得满分，请估计全校九年级有多少学生在此项成绩中获满分．
某校为了解九年级学生的身体素质情况，从全校500名九年级学生中随机抽取了部分学生进行体育测试，其中“跳绳”成绩制成如下频数表和频数直方图：“跳绳”成绩的频数表
| 组别 | 组中值（个） | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
（1）本次抽样调查的样本容量是50，频数表中，a=0.2，b=7c=0.32；
（2）数据分组的组距是10，本次调查的个体是被抽到的每名九年级学生的跳绳成绩；
（3）补全频数直方图；
（4）“跳绳”数在180以上，则此项成绩可得满分，请估计全校九年级有多少学生在此项成绩中获满分．
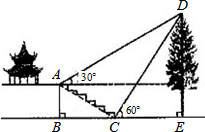如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2m，台阶AC的坡度为1：$\sqrt{3}$，且B，C，E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．