题目内容
11.计算下面各式:(1)$\frac{3tan30°}{3co{s}^{2}30°-2sin30°}$
(2)$\sqrt{8}-4sin45°+{(3-π)^0}+|{\;-4\;}|$.
分析 (1)先利用特殊角的三角函数值得到原式=$\frac{3×\frac{\sqrt{3}}{3}}{3×(\frac{\sqrt{3}}{2})^{2}-2×\frac{1}{2}}$,然后进行乘方运算;
(2)先利用特殊角的三角函数值和零指数幂的意义得到原式=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$+1+4,然后合并即可.
解答 解:(1)原式=$\frac{3×\frac{\sqrt{3}}{3}}{3×(\frac{\sqrt{3}}{2})^{2}-2×\frac{1}{2}}$
=$\frac{\sqrt{3}}{\frac{9}{4}-1}$
=$\frac{4\sqrt{3}}{5}$;
(2)原式=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$+1+4
=2$\sqrt{2}$-2$\sqrt{2}$+1+4
=5.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和特殊角的三角函数值.

练习册系列答案
相关题目
3.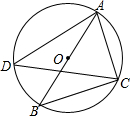 如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )
如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )
 如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )
如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
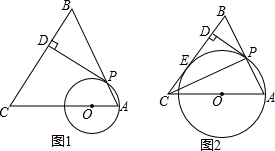
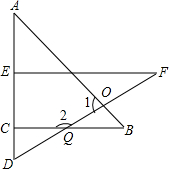 一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30°
一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30°