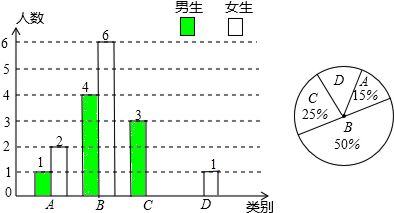
题目内容
3.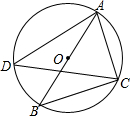 如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )
如图,AB是⊙O的直径,点C、点D在⊙O上,连结AC、BC、AD、CD,若∠BAC=50°,则∠ADC的度数等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
分析 先由直径所对的圆周角为90°,可得:∠ACB=90°,然后由∠BAC=50°,根据三角形内角和定理可得:∠B=40°,然后根据同弧所对的圆周角相等,即可求出∠ADC的度数.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=50°,
∴∠B=40°,
∴∠ADC=∠B=40°.
故选C.
点评 此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,直径所对的圆周角为90°.

练习册系列答案
相关题目
14.已知四边形ABCD是平行四边形,下列结论不正确的是( )
| A. | 当AC=BD时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AB=BC时,它是菱形 |
18.计算(-6)÷(-2)的结果是( )
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
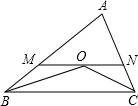 已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.
已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.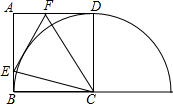 如图,在正方形ABCD中,E是AB边上任意一点,∠ECF=45°,CF交AD于点F,判断直线EF与以C为圆心,CD为半径的圆的位置关系并说明理由.
如图,在正方形ABCD中,E是AB边上任意一点,∠ECF=45°,CF交AD于点F,判断直线EF与以C为圆心,CD为半径的圆的位置关系并说明理由.