题目内容
1.如图1,等腰△ABC中,AC=BC=5,AB=$2\sqrt{5}$,O为腰AC上的一个动点,以O为圆心OA为半径作⊙O交AB于点P,PD⊥BC于点D.(1)求证:PD为⊙O的切线;
(2)如图2,当O点运动到⊙O恰好与BC相切时,设切点为E点,连接CP,求tan∠BCP的值.
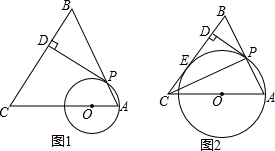
分析 (1)连接OP,先证OP∥BC,得出PD⊥OP,即可得出结论;
(2)连接OE、OP,过C作CF⊥AB于F,先求出∠B的正切值,得出边长关系,再证明四边形OPDE为正方形,设出半径,根据题意列出方程,解方程求出半径,得出CD、FD,即可得出结论.
解答 (1)证明:连接OP,如图1所示: ∵OP=OA,AC=BC,
∵OP=OA,AC=BC,
∴∠OPA=∠A,∠A=∠B,
∴∠OPA=∠B,
∴OP∥BC,
∵PD⊥BC,
∴PD⊥OP,
∴PD为⊙O的切线;
(2)解:连接OE、OP;如图2所示:
过C作CF⊥AB于F,则F为AB的中点,
∴AF=BF=$\sqrt{5}$,
∵AC=BC=5,
∴CF=$\sqrt{{5}^{2}-(\sqrt{5)^{2}}}$=2$\sqrt{5}$,
∴tanA=tanB=$\frac{CF}{BF}$=2,
∵⊙O与BC相切,
∴∠OED=90°,
∴四边形OPDE是矩形,
∵OP=OE,
∴四边形OPDE为正方形
∴OP=OE=PD=ED,设OP=OE=PD=ED=r,
则BD=$\frac{1}{2}$PD=$\frac{r}{2}$,CE=5-$\frac{3r}{2}$,OC=5-r,
在Rt△OCE中,(5-$\frac{3r}{2}$)2+r2=(5-r)2,
解得:r=$\frac{20}{9}$,
∴CD=5-$\frac{1}{2}$r=$\frac{35}{9}$,PD=$\frac{20}{9}$,
∴tan∠BCP=$\frac{PD}{CD}=\frac{20}{35}=\frac{4}{7}$.
点评 本题考查了切线的判定与性质、正方形的判定方法、锐角三角函数、勾股定理的运用;熟练掌握切线的判定与性质,通过设未知数列出方程得出答案是解决问题的关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
12.若5x=2,5y=$\frac{1}{2}$,则x,y之间的关系为( )
| A. | x,y互为相反数 | B. | x,y互为倒数 | C. | x=y | D. | 无法判断 |
9.下列命题是真命题的是( )
| A. | 等腰三角形顶角的外角平分线与底边平行 | |
| B. | 等腰三角形的高、中线、角平分线互相重合 | |
| C. | 底角相等的两个等腰三角形全等 | |
| D. | 等腰三角形的一边不可能是另一边的两倍 |
6.如果船在航标灯的北偏东40°方向上,那么航标灯在船的( )方向上.
| A. | 南偏西40° | B. | 东北方向 | C. | 北偏东50° | D. | 南偏西50° |
10.在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线( )
| A. | 互相垂直 | B. | 互相平行 | C. | 相交 | D. | 相等 |
 如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.
如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.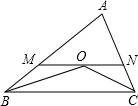 已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.
已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.