题目内容
14.下列条件中,一定能确定两个等腰三角形全等的是( )| A. | 有一腰和底边对应相等的两个等腰三角形 | |
| B. | 有一腰和一角相等的两个等腰三角形 | |
| C. | 有一角和底边相等的两个等腰三角形 | |
| D. | 顶角对应相等的两个等腰三角形 |
分析 此题考查等腰三角形的判定问题,
A中三边相等,可判断全等全等,B中两边及夹角相等,
C中角不确定,不能判断其是否全等,D中角边固定,亦全等.
解答 解:A、有一腰和底边对应相等的两个等腰三角形,即三边对应相等,也可以判断其全等,正确;
B、角与一腰,对应相等,另一腰也相等,两边与一角,不一定证全等,错误;
C、底边固定,角为顶角不可证明其全等,错误;
D、顶角对应相等,不可证全等,错误;
故选A
点评 本题考查了全等三角形的判定与性质及等腰三角形的性质;熟练掌握等腰三角形的性质及判定定理是解决问题的前提.

练习册系列答案
相关题目
4.已知a+3和2a-15是一个数的两个平方根,则这个数是( )
| A. | 4 | B. | 7 | C. | 16 | D. | 49 |
5. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1799 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
2.函数$y=\frac{1}{x-2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x≥2 | D. | x=2 |
9.下列长度的各组线段能组成一个三角形的是( )
| A. | 3cm,5cm,8cm | B. | 1cm,2cm,3cm | C. | 4cm,5cm,10cm | D. | 3cm,4cm,5cm |
3.点P(-2,3)关于y轴的对称点的坐标是( )
| A. | (2,3 ) | B. | (-2,-3) | C. | (-2,3) | D. | (-3,2) |
4.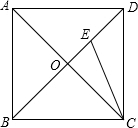 如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )
如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )
 如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )
如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )| A. | 22.5° | B. | 60° | C. | 67.5° | D. | 75° |
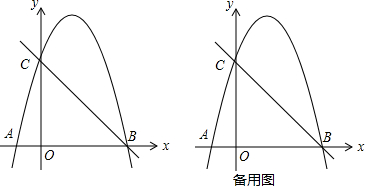 如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)
如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)