题目内容
4．
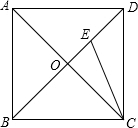如图，正方形ABCD的两条对角线AC，BD相交于点O，点E在BD上，且BE=CD，则∠BEC的度数为（ ）| A． | 22.5° | B． | 60° | C． | 67.5° | D． | 75° |
分析 由正方形的性质得到BC=CD，∠DBC=45°，证出BE=BC，根据三角形的内角和定理求出∠BEC=∠BCE=67.5°即可．
解答 解：∵四边形ABCD是正方形，
∴BC=CD，∠DBC=45°，
∵BE=CD，
∴BE=BC，
∴∠BEC=∠BCE=（180°-45°）÷2=67.5°，
故选C．
点评 本题考查了正方形的性质，三角形的内角和定理，等腰三角形的性质等知识；熟练掌握正方形的性质，证出BE=BC是解决问题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
14．下列条件中，一定能确定两个等腰三角形全等的是（ ）
| A． | 有一腰和底边对应相等的两个等腰三角形 | |
| B． | 有一腰和一角相等的两个等腰三角形 | |
| C． | 有一角和底边相等的两个等腰三角形 | |
| D． | 顶角对应相等的两个等腰三角形 |
据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪，如平面几何图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°（tan31°≈0.6，tan50°≈1.2，结果精确到1m）
12．下列图形中既是中心对称图形又是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．-$\root{3}{-64}$的平方根是（ ）
| A． | 2 | B． | ±2 | C． | ±4 | D． | 不存在 |
16．
如图，数轴上点P表示的数可能是（ ）
如图，数轴上点P表示的数可能是（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{5}$ | C． | $\sqrt{10}$ | D． | $\sqrt{15}$ |
14．据报道，2015年我国每千名儿童所拥有的儿科医生数为0.43（将0～14岁的人群定义为儿童），远低于世界主要发达国家，儿科医生存在较大缺口．根据2000-2015年报道的相关数据，绘制统计图表如下：
全国人口、儿童人口、儿科医生及每千名儿童拥有的儿科医生数统计表
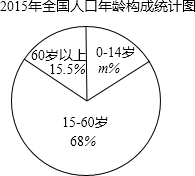
根据以上信息解答下列问题：
（1）直接写出扇形统计图中m的值；
（2）根据统计表估计2020年我国人口数约为14亿人；
（3）若2020年我国儿童占总人口的百分比与2015年相同，请你估算到2020年我国儿科医生需比2015年增加多少万人，才能使每千名儿童拥有的儿科医生数达到0.6．
全国人口、儿童人口、儿科医生及每千名儿童拥有的儿科医生数统计表
| 年份 | 全国人口 （亿人） | 儿童人口 （亿人） | 儿科医生 （万人） | 每千名儿童拥有的儿科医生数 |
| 2000 | 12.67 | 2.9 | 9.57 | 0.33 |
| 2005 | 13.06 | 2.65 | 10.07 | 0.38 |
| 2010 | 13.4 | 2.22 | 10.43 | 0.47 |
| 2015 | 13.7 | 2.26 | 9.72 | 0.43 |
根据以上信息解答下列问题：
（1）直接写出扇形统计图中m的值；
（2）根据统计表估计2020年我国人口数约为14亿人；
（3）若2020年我国儿童占总人口的百分比与2015年相同，请你估算到2020年我国儿科医生需比2015年增加多少万人，才能使每千名儿童拥有的儿科医生数达到0.6．