题目内容
若方程x2+2x+11-k（x-3）=0的两个根都大于2，试求k的取值范围．
考点：一元二次方程根的分布
专题：
分析：利用二次函数的零点与判别式、对称轴及区间端点处的函数值的关系即可得出．
解答：解：由原方程，得
x2+（2-k）x+11+3k=0
令y=x2+（2-k）x+11+3k
∵方程x2+2x+11-k（x-3）=0，即x2+（2-k）x+11+3k=0的两个根都大于2，
∴
，
整理，得
，
解得k≥8+2
．
∴实数k的取值范围是k≥8+2
．
x2+（2-k）x+11+3k=0
令y=x2+（2-k）x+11+3k
∵方程x2+2x+11-k（x-3）=0，即x2+（2-k）x+11+3k=0的两个根都大于2，
∴
|
整理，得
|
解得k≥8+2
| 26 |
∴实数k的取值范围是k≥8+2
| 26 |
点评：此题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
如图，AD∥BC，AD=BC，AE=CF．求证：
如图，△ABC的高BD、CE相交于点H，现给出四个判断：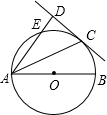
如图，已知AB是⊙O的直径，点E为⊙O上一点，且AC平分∠BAE交⊙O于C，过C作CD⊥AE，垂足为D．