题目内容
已知抛物线y=x2+kx+2k-4,若抛物线与x轴交于A(x1,0),B(x2,0),与y轴交于点C(A为定点且点A在B的左侧),且S△ABC=15.求k的值.
考点:抛物线与x轴的交点
专题:
分析:首先判断是否存在第四个交点,由题干条件|x1|<|x2|或者|x1|<|x2|,显然抛物线的对称轴不是y轴,即C点不可能是抛物线的顶点(因为点C不在抛物线的对称轴上),所以解题的关键就转化为如何求k的值,可以从△ABC的面积入手.先得到k的取值范围,进而通过△ABC的面积求出k的值.
解答:解:令y=0,有x2+kx+2k-4=0,
此一元二次方程根的判别式
△=k2-4•(2k-4)=k2-8k+16=(k-4)2,
∵无论k为什么实数,(k-4)2≥0,
方程x2+kx+2k-4=0都有解,
即抛物线总与x轴有交点.
由求根公式得x=
,
当k≥4时,x=
,x1=
=-2,x2=
=-k+2;
当k<4时,x=
,x1=
=-k+2,x2=
=-2.
即抛物线与x轴的交点分别为(-2,0)和(-k+2,0),
故点A(-2,0)是x轴上的定点.
当-2<-k+2,即k<4时,A点坐标为(-2,0),B为(-k+2,0).
即x1=-2,x2=-k+2.
由|x1|<|x2|得-k+2>2,解得k<0.
根据S△ABC=15,得
AB•OC=15.
AB=-k+2-(-2)=4-k,
OC=|2k-4|=4-2k,
∴
(4-k)(4-2k)=15,
化简整理得k2-6k-7=0,
解得k=7(舍去)或k=-1.
此一元二次方程根的判别式
△=k2-4•(2k-4)=k2-8k+16=(k-4)2,
∵无论k为什么实数,(k-4)2≥0,
方程x2+kx+2k-4=0都有解,
即抛物线总与x轴有交点.
由求根公式得x=
| -k±|k-4| |
| 2 |
当k≥4时,x=
| -k±(k-4) |
| 2 |
| -k+(k-4) |
| 2 |
| -k-(k-4) |
| 2 |
当k<4时,x=
| -k±(4-k) |
| 2 |
| -k+(4-k) |
| 2 |
| -k-(4-k) |
| 2 |
即抛物线与x轴的交点分别为(-2,0)和(-k+2,0),
故点A(-2,0)是x轴上的定点.
当-2<-k+2,即k<4时,A点坐标为(-2,0),B为(-k+2,0).
即x1=-2,x2=-k+2.
由|x1|<|x2|得-k+2>2,解得k<0.
根据S△ABC=15,得
| 1 |
| 2 |
AB=-k+2-(-2)=4-k,
OC=|2k-4|=4-2k,
∴
| 1 |
| 2 |
化简整理得k2-6k-7=0,
解得k=7(舍去)或k=-1.
点评:该题的难度较大,主要涉及了:二次函数与方程的关系以及不等式的应用等综合知识,k的取值范围的确定是本题的难点所在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
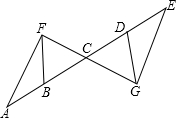 如图,CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上.求证:
如图,CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上.求证: