Question

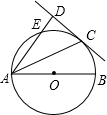如图，已知AB是⊙O的直径，点E为⊙O上一点，且AC平分∠BAE交⊙O于C，过C作CD⊥AE，垂足为D．
（1）求证：CD为⊙O的切线；
（2）若⊙O的直径为10，圆心O到AD的距离为4，求AE和ED的长度．

Answer 1

考点：切线的判定与性质

专题：

分析：（1）通过角平分线和有两半径为边的三角形是等腰三角形可得到OC∥AD，再证明OC⊥CD．
（2）如图2，过点O作OH⊥AD于点H．利用勾股定理求得AH=3，则由垂径定理来求AE的长度；通过△ADC∽△ACB的对应边成比例求得AD的长度，则DE=AD-AE．

解答：（1）证明：连OC，BC，如图1，
∵AC平分∠BAE，
∴∠1=∠2，
∵OA=OC，
∴∠2=3，
∴∠1=∠3，
∴AD∥OC．
又∵CD⊥AE，
∴OC⊥CD．
又∵OC是圆O的半径，
∴PC是⊙O的切线．

（2）解：如图2，连接OD、OC、BC．
由（1）知，OC⊥CD．
∵AD⊥CD，
∴OC∥AD．
过点O作OH⊥AD于点H，则四边形DHOC是矩形，且OH═CD=4，AE=2AH．
∵⊙O的直径AB为10，
∴OA=5，
∴在直角△AOH中，由勾股定理得到：AH=

AO2-OH2

=

52-42

=3，
∴AE=2AH=6．
∵∠ADC=∠ACB=90°，∠DAC=∠DAB，
∴△ADC∽△ACB，
∴

AD

AC

=

AC

AB

，即

AD

AC

=

AC

10

，则AC²=10AD．
又由勾股定理得到：AC²=AD²+CD²，
∴AD²-10AD+16=0．
解得 AD=8或AD=2（舍去），
故DE=AD-AE=8-6=2．
综上所述，AE和ED的长度分别是6、2．

点评：本题考查了切线的判定与性质，证明切线的问题转化为证明线段垂直的问题．要学会充分利用特殊角进行角度计算，确定边之间的数量．