题目内容
4.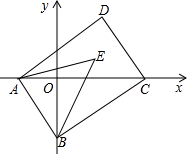 如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:
如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:(1)求A、B两点的坐标;
(2)设四边形ABCD的面积满足9<S四边形ABCD<15,求m的取值范围;
(3)分别作∠OAD、∠OBC的平分线AE、BE,交点为E,请直接写出∠AEB的度数(不必说明理由).
分析 (1)利用非负性转化成两个方程,求出a,b,从而确定出点A,B坐标;
(2)先确定出S△ABC=S△ADC,再求出四边形的面积的范围建立不等式组,求解即可,
(3)利用平移和直角三角形两锐角互余,求出,∠DAC+∠OBC=90°,再借助角平分线求出,∠EAC+∠CBE=45°.从而求出,∠EAB+∠EBA=135°.
解答 解:(1)∵(3a-2b)2+|a-b-1|=0,
∴3a-2b=0,a-b-1=0,
∴a=-2,b=-3,
∴A(-2,0),B(0,-3);
(2)∵B(0,-3),
∴OB=3,
∵将线段AB平移到DC,连接对应点A、D和B、C,
∴S△ABC=S△ADC,
∴S四边形ABCD=2S△ABC=2×$\frac{1}{2}$AC×OB=3(m+2),
∵9<S四边形ABCD<15,
∴9<3(m+2)<15,
∴1<m<3;
(3)由平移得,AD∥BC,
∴∠DAB+∠CBA=180°,
∴∠DAC+∠OAB+∠ABO+∠OBC=180°,
∵∠OAB+∠ABO=90°,
∴∠DAC+∠OBC=90°,
∵∠OAD、∠OBC的平分线AE、BE,交点为E,
∴2∠EAC=∠DAC,2∠CBE=∠CBO,
∴∠EAC+∠CBE=45°,
∵∠OAB+∠ABO=90°,
∴∠EAB+∠EBA=90°+45°=135°,
∴∠AEB=180°-(∠EAB+∠EBA)=180°-135°=45°.
点评 此题是几何变换综合题,主要考查了,非负性的应用,面积的计算,解不等式组,解方程,角平分线的性质,直角三角形的直线,解本题的关键,非负性的应用和判定∠EAC+∠CBE=45°.

练习册系列答案
相关题目
12.数据-1,2,3,0,1的平均数( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.下列各式正确的是( )
| A. | $\sqrt{16}$=±4 | B. | ±$\sqrt{16}$=4 | C. | $\sqrt{(-4)^{2}}$=-4 | D. | $\root{3}{-27}$=-3 |
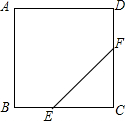 如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.
如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.
 如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解.
如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解. 如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.