题目内容
13. 如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.(1)证明:△ACD≌△BCE;
(2)求∠AEB的度数.
分析 (1)先由等边三角形的性质判断出∠ACD=∠BCE,再用SAS判断出结论;
(2)由(1)结论得到∠ADC=∠BEC,再用邻补角求出∠AEB的度数.
解答 解:(1)∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE,
(2)由(1)得,△ACD≌△BCE,
∴∠ADC=∠BEC,
∵∠ADC+∠CDE=180°,∠CDE=60°,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
点评 此题是全等三角形的判定与性质,主要考查了等边三角形的性质,邻补角,解本题的关键是判断出∠ACD=∠BCE.

练习册系列答案
相关题目
1.玄武区四月份第一周连续七天的空气质量指数(AQI)分别为:128,97,60,72,66,69,86.则这七天空气质量变化情况最适合用哪种统计图描述( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上都不对 |
3.小颖用长度为奇数的三根木棒搭一个三角形,其中两根木棒的长度分别为9cm和3cm,则第三根木棒的长度是( )
| A. | 5cm | B. | 9cm | C. | 10cm | D. | 13cm |
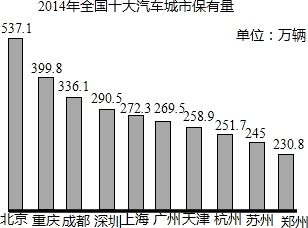 2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.
2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.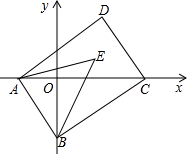 如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:
如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题: 如图,一转盘被平均分成8份,转动指针,停止后指针指向的数字即为转出的数字.现有两种规则:规则A:甲方猜“是正数”,乙方猜“是负数”;规则B:甲方猜“是负整数”,乙方猜“是分数”;请问哪个规则公平?规则A和规则B.
如图,一转盘被平均分成8份,转动指针,停止后指针指向的数字即为转出的数字.现有两种规则:规则A:甲方猜“是正数”,乙方猜“是负数”;规则B:甲方猜“是负整数”,乙方猜“是分数”;请问哪个规则公平?规则A和规则B. 关于x的一元二次方程a2x2+2ax-3=0(a≠0).
关于x的一元二次方程a2x2+2ax-3=0(a≠0).