题目内容
12.计算:(1)1-$\frac{1}{{2}^{2}}$=$\frac{3}{4}$;
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)=$\frac{2}{3}$;
(3)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)=$\frac{5}{8}$;
请你利用你找到的简便方法计算:
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{4}^{2}}$)(1-$\frac{1}{201{5}^{2}}$).
分析 利用平方差公式计算找出计算规律解决问题即可.
解答 解:(1)1-$\frac{1}{{2}^{2}}$=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)=$\frac{1}{2}$×$\frac{3}{2}$=$\frac{3}{4}$;
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$=$\frac{2}{3}$;
(3)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$=$\frac{5}{8}$;
请你利用你找到的简便方法计算:
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{4}^{2}}$)(1-$\frac{1}{201{5}^{2}}$)
=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{2014}$)(1+$\frac{1}{2014}$)(1-$\frac{1}{2015}$)(1+$\frac{1}{2015}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{2013}{2014}$×$\frac{2015}{2014}$×$\frac{2014}{2015}$×$\frac{2016}{2015}$
=$\frac{1008}{2015}$.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案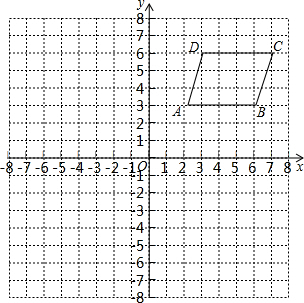 如图,建立平面直角坐标系,点A、B、C、D都在方格的格点上,
如图,建立平面直角坐标系,点A、B、C、D都在方格的格点上,①分别写出A、B、C、D的坐标;
②把四边形ABCD平移,使点C平移到点(-2,4)处,画出平移后的四边形;
③求平行四边形ABCD的面积.
| A. | $\sqrt{8}$与$\sqrt{9}$之间 | B. | 6与7之间 | C. | 7与8之间 | D. | 8与9之间 |
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
 如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2.
如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2.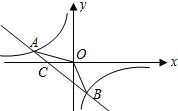 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.