题目内容
12.已知:$\frac{a}{b}$=$\frac{c}{d}$,求证:$\frac{b-a}{b}$=$\frac{d-c}{d}$.分析 根据等式的性质2:等式的两边都乘以(或除以)同一个不为零的数,结果不变,可得-$\frac{a}{b}$=-$\frac{c}{d}$,再根据等式的性质1:等式的两边都加上(或减去)同一个数,结果不变,可得答案.
解答 证明:∵$\frac{a}{b}$=$\frac{c}{d}$,
∴-$\frac{a}{b}$=-$\frac{c}{d}$,
∴1-$\frac{a}{b}$=1-$\frac{c}{d}$,
即$\frac{b-a}{b}$=$\frac{d-c}{d}$.
点评 本题考查了比例的性质,利用了等式的性质:等式的两边都乘以(或除以)同一个不为零的数,结果不变;等式的两边都加上(或减去)同一个数,结果不变.

练习册系列答案
相关题目
1.(1)填表:
(2)在同一直角坐标系中,作出上述三个函数的图象;
(3)它们三者的图象有什么异同?它们的开口方向、对称轴、顶点坐标分别是多少?
(4)由抛物线y=-2x2怎样平移得到抛物线y=-2x2+1与y=-2x2-1?
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | |||||||
| y=-2x2+1 | |||||||
| y=-2x2-1 |
(3)它们三者的图象有什么异同?它们的开口方向、对称轴、顶点坐标分别是多少?
(4)由抛物线y=-2x2怎样平移得到抛物线y=-2x2+1与y=-2x2-1?
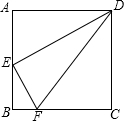 如图所示,已知正方形ABCD的周长为16cm,E为AB的中点,F为BC上一点,且BF:FC=1:3,求△DEF的周长和面积.
如图所示,已知正方形ABCD的周长为16cm,E为AB的中点,F为BC上一点,且BF:FC=1:3,求△DEF的周长和面积.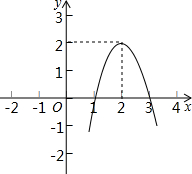 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
 有理数a,b,c在数轴上的位置如图所示,化简:-|a|+|b|-|0|-|c|.
有理数a,b,c在数轴上的位置如图所示,化简:-|a|+|b|-|0|-|c|.