题目内容
7.在Rt△ABC中,∠C=90°.∠B=60°.DE是斜边AB的垂直平分线,且DE=2.则AC的长为6.分析 先求出∠DBC=30°,根据含30°角的直角三角形性质求出AD=2DE,BD=2CD,根据线段垂直平分线性质求出AD=BD,即可求出答案.
解答 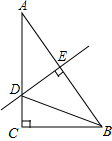
解:∵在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,
∵DE是斜边AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=30°,
∴∠DBC=60°-30°=30°,
∵DE=2,
∴AD=2DE=4,BD=AD=4,
∴CD=$\frac{1}{2}$BD=2,
∴AC=4+2=6.
故答案为:6.
点评 本题考查了线段垂直平分线性质,等腰三角形性质,三角形内角和定理,含30°角的直角三角形性质的应用,能灵活运用含30°角的直角三角形性质求出AD、CD的长是解此题的关键.

练习册系列答案
相关题目
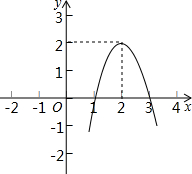 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
