题目内容
16.已知a=$\sqrt{3}$+1,求代数式:(4-2$\sqrt{3}$)a2+(1-$\sqrt{3}$)a的值.分析 根据完全平方式的特点把4-2$\sqrt{3}$化成($\sqrt{3}$-1)2的形式,再代入a的值运用平方差公式计算,即可得出结果.
解答 解:∵a=$\sqrt{3}$+1,
∴(4-2$\sqrt{3}$)a2+(1-$\sqrt{3}$)a
=($\sqrt{3}$-1)2a2-($\sqrt{3}$-1)a
=[($\sqrt{3}$-1)a]2-($\sqrt{3}$-1)a
=[($\sqrt{3}$-1)($\sqrt{3}$+1]2-($\sqrt{3}$-1)($\sqrt{3}$+1)
=(3-1)2-(3-1)
=4-2
=2.
点评 本题考查了二次根式的化简求值、完全平方公式、平方差公式;熟练掌握完全平方公式和平方差公式是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.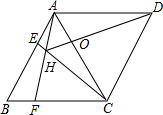 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
4.已知等腰三角形的两边长是5cm和6cm,则此三角形的周长是( )
| A. | 16cm | B. | 17cm | C. | 11cm | D. | 16cm或17cm |
8.二元一次方程2x+y=7的正整数解的个数有( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.
如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.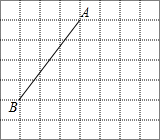 线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.