题目内容
5．
如图，四边形ABCD是平行四边形，对角线AC，BD相交于点O，且∠1=∠2．求证：四边形ABCD是矩形．
分析 根据等角对等边得出OB=OC，根据平行四边形性质求出OC=OA=$\frac{1}{2}$AC，OB=OD=$\frac{1}{2}$BD，推出AC=BD，根据矩形的判定推出即可．
解答 证明：在?ABCD中，AO=CO，BO=DO，
∵∠1=∠2，
∴BO=CO，
∴AO=BO=CO=DO，
∴AC=BD，
∴?ABCD为矩形．
点评 本题考查了平行四边形的性质，等腰三角形的判定，矩形的判定，注意：对角线相等的平行四边形是矩形，等角对等边．
练习册系列答案
相关题目
在△ABC中，AB=AC=14cm，D为BA的中点，DE⊥AB交BC于E．若△EBC的周长为25cm，则BC长为11cm．
如图，三角形ABC中，∠BAC=70°，点D是射线BC上一点（不与点B、C重合），DE∥AB交直线AC于E，DF∥AC交直线AB于F，则∠FDE的度数为70°或110°．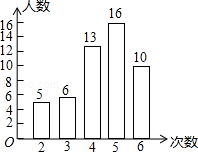
我市开展了“寻找雷锋足迹”的活动，某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况，随机调查了八年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有（ ）
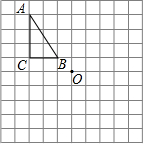已知，如图△ABC，请在网格纸中画．
如图，在△ABC中，AD是角平分线，点E在AB上，且DE∥CA．