题目内容
16.边长为2,2,2$\sqrt{2}$的三角形是等腰直角三角形.分析 首先根据2=2,可得该三角形是等腰三角形;然后根据${2}^{2}{+2}^{2}=8{,(2\sqrt{2})}^{2}=8$,可得该三角形是直角三角形,所以边长为2,2,2$\sqrt{2}$的三角形是等腰直角三角形,据此解答即可.
解答 解:∵2=2,
∴该三角形是等腰三角形;
∵${2}^{2}{+2}^{2}=8{,(2\sqrt{2})}^{2}=8$,
∴${2}^{2}{+2}^{2}{=(2\sqrt{2})}^{2}$,
∴该三角形是直角三角形,
∴边长为2,2,2$\sqrt{2}$的三角形是等腰直角三角形.
故答案为:等腰直角.
点评 此题主要考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.下列几何图形不是中心对称图形的是( )
| A. | 线段 | B. | 等边三角形 | C. | 正方形 | D. | 圆 |
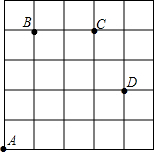 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向. 如图,在平面直角坐标中,一直线与x轴相交于点A(8,0),与y轴交于B(0,6),P是线段AB上一动点(不与A,B重合),过P分别作出x轴和y轴的垂线,垂足为M,N.
如图,在平面直角坐标中,一直线与x轴相交于点A(8,0),与y轴交于B(0,6),P是线段AB上一动点(不与A,B重合),过P分别作出x轴和y轴的垂线,垂足为M,N.