题目内容
1.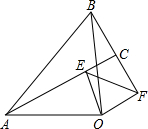 如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明:
如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明:(1)AE=BF;
(2)AE⊥BF.
分析 (1)由∠AOB=∠EOF=90°得∠AOE=∠BOF,根据SAS即可判定△AOE≌△BOF.
(2)由△AOE≌△BOF得∠OAE=∠OBF,因为∠OAG+∠AGO=90°,∠AGO=∠BGC,所以∠BGC+∠GBC=90°,即∠BCG=90°得证.
解答 (1)证明:如图AC与BO交于点G,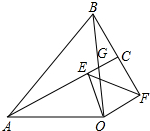
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
在△AOE和△BOF中,
$\left\{\begin{array}{l}{AO=OB}\\{∠AOE=∠BOF}\\{OE=OF}\end{array}\right.$,
∴△AOE≌△BOF.
(2)∵△AOE≌△BOF,
∴∠OAE=∠OBF,
∵∠OAG+∠AGO=90°,∠AGO=∠BGC,
∴∠BGC+∠GBC=90°,
∴∠BCG=90°,
∴AC⊥BF.
点评 本题考查全等三角形的判定和性质、等角的余角相等,本题提供了“8字型”证明90°一个方法,属于中考常考题型.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
7.某天中午的气温是8℃,记作+8℃,晚上的气温是零下2℃,则这天晚上的气温可记作( )
| A. | +2℃ | B. | 1℃ | C. | -2℃ | D. | -1℃ |
11. 如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
 如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )| A. | 3米 | B. | 4米 | C. | 5米 | D. | 6米 |
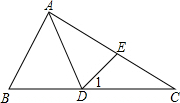 如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.
如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.
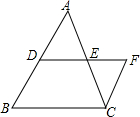 如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?
如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?
 如图,已知线段a,请用尺规作图,并填空(不写作法,但要保留作图痕迹)
如图,已知线段a,请用尺规作图,并填空(不写作法,但要保留作图痕迹)