题目内容
8.(1)计算:$sin60°cos30°+\sqrt{2}sin45°-tan45°$(2)解方程:x2-2x-2=0.
分析 (1)直接利用特殊角的三角函数值代入求出即可.
(2)把常数项-2移项后,应该在左右两边同时加上一次项系数-4的一半的平方.
解答 解:(1)原式=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-1
=$\frac{3}{4}$+1-1
=$\frac{3}{4}$;
(2)x2-2x-2=0,
x2-2x=2,
x2-2x+1=3,
(x-1)2=3,
x-1=±$\sqrt{3}$,
解得x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$.
点评 此题主要考查了特殊角的三角函数值,配方法解方程.用配方法解一元二次方程的步骤:
(1)形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.
(2)形如ax2+bx+c=0型,方程两边同时除以二次项系数,即化成x2+px+q=0,然后配方.

练习册系列答案
相关题目
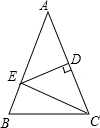 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.求∠ECB的度数.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.求∠ECB的度数.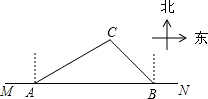 2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?
2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?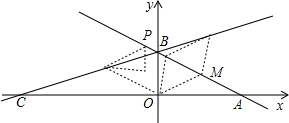 如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.
如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.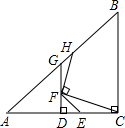 如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.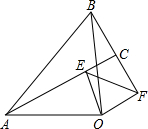 如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明:
如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明: