题目内容
13.【问题提出】如何把n个边长为1的小正方形,剪拼成一个大正方形?【探究一】若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成个大正方形.
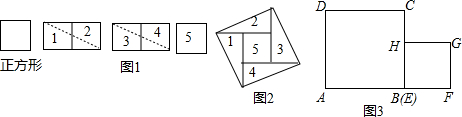
请你用9个边长为1的小正方形拼成一个大正方形.(如图正方形)
【探究二】若n=2、5、10、13等,这些数,都可以用两个正整数平方和的算术平方根来表示,如:2=$\sqrt{{1}^{2}{+1}^{2}}$;5=$\sqrt{{2}^{2}{+1}^{2}}$.
解决方法:以n=5为例
(1)计算:拼成的大正方形的面积是5,边长为$\sqrt{5}$;
(2)剪切:如图1,将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图1中的虚线为边,拼成一个边长为$\sqrt{5}$的大正方形,如图2.
请你仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积是13,边长为$\sqrt{13}$;
(2)剪切:请画出剪切的图形;
(3)拼图:请画出拼成的图形;
【问题拓展】如图3,给你两个大小不相等的正方形ABCD和EFGH,设正方形ABCD的边长为a,正方形EFGH的边长为b.
请你仿照上面的研究方式,把它剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积是a2+b2,边长为$\sqrt{{a}^{2}{+b}^{2}}$;
(2)剪切:请在图3中完成;
(3)拼图:请画出拼成的图形.
分析 探究一:由大正方形的面积计算出边长,从而可画出图形;
探究二:将13正正方形分割为1个边长为1的正方形和4个两直角边分别为2和3的直角三角形即可;
探究三:将两个正方形分割为1个边长为(a-b)的正方形和4个两直角边分别为a和b的直角三角形即可.
解答 解:探究一:∵9个边长为1的正方形的面积为9,
∴所拼成的正方形的边长为3.
所拼图形如图所示: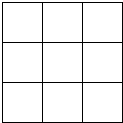
探究二:(1)$\sqrt{13}$=$\sqrt{{2}^{2}+{3}^{2}}$;
(2)如图所示: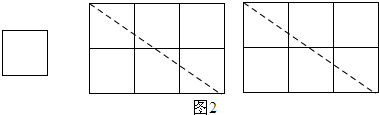
(3)拼成的图形如图所示: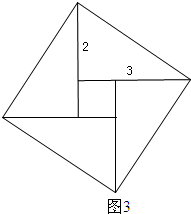
探究三:(1)计算:拼成的大正方形的面积是a2+b2,边长为$\sqrt{{a}^{2}{+b}^{2}}$;
(2)如图4所示: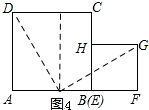
(3)拼成的图形如图5所示: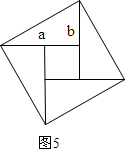
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了正方形的性质,正方形的面积公式、勾股定理,能够将所给图形分割为1个正方形和4个直角三角形是解题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
3.已知三角形的两边长分别为8和4,则第三边长可能是( )
| A. | 3 | B. | 4 | C. | 8 | D. | 12 |
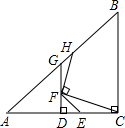 如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.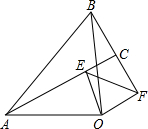 如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明:
如图,已知等腰三角形OAB、OEF中,∠AOB=90°,∠EOF=90°,连接AE、BF,说明: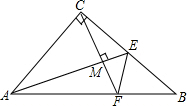 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证: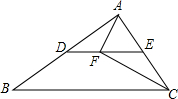 如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.
如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.