题目内容
10.先化简再求值:(x2+3x)(x-3)-x(x-2)2+(x-y)(y-x),其中x=3,y=-2.分析 第一项提取公因式x,然后根据平方差公式和完全平方公式分别进行计算,化简后再把x、y的值代入进行计算即可得解.
解答 解:(x2+3x)(x-3)-x(x-2)2+(x-y)(y-x),
=x(x+3)(x-3)-x(x2-4x+4)-(x-y)(x-yx),
=x(x2-9)-x3+4x2-4x-(x2-2xy+y2),
=x3-9x-x3+4x2-4x-x2+2xy-y2,
=3x2-13x-y2+2xy,
当x=3,y=-2时,原式=3×32-13×3-(-2)2+2×3×(-2),
=27-39-4-12,
=27-55,
=-28.
点评 本题考查的是整式的混合运算,主要利用了平方差公式,完全平方公式,整式的加减混合运算,熟记公式与运算法则并准确化简是解题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | x2+x3=x5 | B. | (x4)2=x6 | C. | x6÷x2=x3 | D. | (-x5)4=x20 |
15.一艘轮船以18海里/时沿北偏东60°的方向航行,上午九时,测得小岛A在正东方向,3小时后,看见小岛在南偏东30°方向上,此时船与小岛的距离为( )
| A. | 27$\sqrt{2}$海里 | B. | 18$\sqrt{3}$海里 | C. | 27$\sqrt{3}$海里 | D. | 18$\sqrt{2}$海里 |
20. 如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )
如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )
 如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )
如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )| A. | 80° | B. | 90° | C. | 100° | D. | 102° |
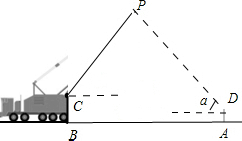 如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$)
如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$)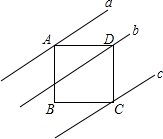 如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( )
如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( )