题目内容
17.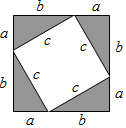 如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2.
如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2.
分析 先求得大正方形的边长,然后依据面积公式可求得大正方形的面积,然后依据大正方形的面积=小正方形的面积+4个直角三角形的面积可得到大正方形的面积,然后依据大正方形的面积列出等式,然后可得到a、b、c之间的关系.
解答 解:大正方形的面积=(a+b)2,大正方形的面积=2ab+c2,则(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.
故答案为:(a+b)2;2ab+c2;(a+b)2=2ab+c2;a2+b2=c2.
点评 本题主要考查的是勾股定理的证明,利用不同的方法表示出大正方形的面积是解题的关键.

练习册系列答案
相关题目
2.若0<a<1,则不等式(x-a)(x-$\frac{1}{a}$)<0的解为( )
| A. | {x|a<x<$\frac{1}{a}$} | B. | {x|$\frac{1}{a}$<x<a} | C. | {x|x<a或x>$\frac{1}{a}$} | D. | {x|x<$\frac{1}{a}$或x>a} |
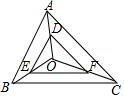 如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗?说明理由.
如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗?说明理由.

 如图,△ABC中,∠ACB=90°,AC=BC,BD⊥BC于B,点E在 BC上,CE=BD,DC、AE交于点F.试问DC与AE有何关系,请说明理由.
如图,△ABC中,∠ACB=90°,AC=BC,BD⊥BC于B,点E在 BC上,CE=BD,DC、AE交于点F.试问DC与AE有何关系,请说明理由.