题目内容
5.已知不等式ax2+bx+c>0的解是α<x<β,其中β>α>0,求不等式cx2+bx+α<0的解.分析 利用已知条件求出cx2+bx+a=0的两根,比较大小,写出解集.
解答 解:由题意知a<0,且α,β为方程ax2+bx+c=0的两根,则$\left\{\begin{array}{l}{α<0}\\{α+β=-\frac{b}{a}}\\{αβ=\frac{c}{a}}\end{array}\right.$,
设cx2+bx+a=0的两根为x,和x2(x1<x2)则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-\frac{b}{c}=\frac{α+β}{αβ}=\frac{1}{β}+\frac{1}{α}}\\{{x}_{1}{x}_{2}=\frac{a}{c}=\frac{1}{αβ}=\frac{1}{α}•\frac{1}{β}}\end{array}\right.$,
∵0<α<β,
∴$\frac{1}{β}$<$\frac{1}{α}$,
∴x1=$\frac{1}{β}$,x2=$\frac{1}{α}$,
又∵c<0,
∴cx2+bx+a<0,
解集是{x|x1<$\frac{1}{β}$或x2>$\frac{1}{α}$}.
点评 本题考查一元二次不等式的解,关键是知道一元二次不等式解集和对应的一元二次方程之间解的联系.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、C的坐标分别为(0,-$\sqrt{2}$)、(2$\sqrt{2}$,0),将矩形OABC绕点O顺时针旋转45°得到矩形OA′B′C′,边A′B′与y轴交于点D,经过坐标原点的抛物线y=ax2+bx同时经过点A′、C′.
如图,在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、C的坐标分别为(0,-$\sqrt{2}$)、(2$\sqrt{2}$,0),将矩形OABC绕点O顺时针旋转45°得到矩形OA′B′C′,边A′B′与y轴交于点D,经过坐标原点的抛物线y=ax2+bx同时经过点A′、C′. 如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.
如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.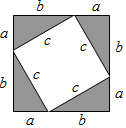 如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2.
如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2. 如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30.
如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30.