题目内容
15.市政府决定对市区某路段进行扩建,现从甲乙两个工程队提供的资料可知,若两队合做,24天可以完工,若两队合做8天后,再由乙队独做40天也能完工,现在甲队每天的施工费用为3万元,乙队每天的施工费用为1.5万元.(1)甲乙两队单独施工各需要多少天完成工程?
(2)根据工程预算,总费用不得超过114万元,而现在接到大运会组委会通知,要求该工程不超过30天完工,请你帮忙决策,至少让乙队参与施工多少天?
分析 (1)本题是一个有关于二元一次的分式方程.若两个工程队合作24天恰好完成;若两个工程队合作8天后,乙工程队再单独做40天,也恰好完成.可得出两个等量关系:甲24天完成工作量+乙24天工作量=1;甲乙合作88天的工作量+乙单独做40天的工作量=1,由此可列出方程组求解.
(2)可由该工程不超过30天完工、甲乙两队的工作量之和为1及总费用不超过114万元的不等关系进行分析.
解答 解:(1)设甲队单独施工需要x天完成工程,乙队单独施工需要y天完成工程,依题意得:
$\left\{\begin{array}{l}{\frac{24}{x}+\frac{24}{y}=1}\\{(\frac{1}{x}+\frac{1}{y})×8+\frac{40}{y}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=60}\end{array}\right.$,
经检验,$\left\{\begin{array}{l}{x=40}\\{y=60}\end{array}\right.$是原方程的解,且符合题意.
答:甲队单独施工需要40天完成工程,乙队单独施工需要60天完成工程.
(2)设甲队参与施工a天,乙队参与施工b天时,总的施工费用不超过114万元.
根据题意得:$\left\{\begin{array}{l}{a≤30}\\{b≤30}\\{\frac{a}{40}+\frac{b}{60}=1}\\{3a+1.5b≤114}\end{array}\right.$,
解得:b≥12.
答:至少让乙队参与施工12天.
点评 本题考查了分式方程的应用.列方程解应用题的步骤是:一审(审题)二设(设出相应未知数)三列(根据等量关系和所设未知数列出方程)四解(解方程)五检验(检验是否是方程的解,是否符合实际问题含义)六回答(根据所问的进行回答),其中审题时找出等量关系是列方程解决实际问题的关键.

| A. | $\frac{1}{4}$b2-2ab2-4a2 | B. | $\frac{1}{4}$b4-2ab2+4a2 | C. | $\frac{1}{4}$b2ab2+4a2 | D. | -$\frac{1}{4}$b4+ab2-4a2 |

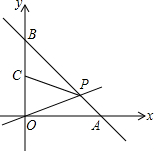 已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.
已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.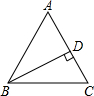 如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.