题目内容
13.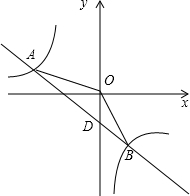 在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.
在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.(1)求S△OBD;
(2)求S△AOB.
分析 根据一次函数经过A(-3,1),B(1,-3)两点,求出直线AB的解析式,求出点D的坐标,根据三角形面积公式求出S△OBD和S△AOB的面积.
解答 解:(1)设直线AB的解析式为y=kx+b,
由题意得,
$\left\{\begin{array}{l}{-3k+b=1}\\{k+b=-3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
∴直线AB的解析式为:y=-x-2,
则点D的坐标为(0,-2)
∴S△OBD=$\frac{1}{2}$×2×1=1;
(2)S△AOB=S△OBD+S△OAD
=1+$\frac{1}{2}$×2×3
=4.
点评 本题考查的是一次函数与反比例函数的交点问题,掌握待定系数法求函数解析式的一般步骤是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
4.已知等腰三角形的周长为24,腰长为x,则x的取值范围是( )
| A. | x>12 | B. | x<6 | C. | 6<x<12 | D. | 0<x<12 |
8.若(2m-4)x|2m-3|=8是关于x的一元一次方程,则m的值是( )
| A. | 任何数 | B. | 1 | C. | 2 | D. | 1或2 |
18.李老师给出:(a-b)2=5,a2+b2=2,你能计算出ab的值为( )
| A. | -1 | B. | 3 | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
3.支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北,据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学记数法表示为( )
| A. | 4.73×1010 | B. | 47.3×1010 | C. | 4.73×109 | D. | 47.3×109 |
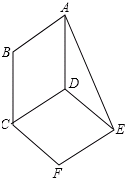 如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.
如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.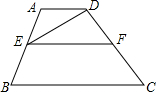 如图,∵∠ADE=∠DEF(已知),
如图,∵∠ADE=∠DEF(已知), 仔细观察三角系数表,按规律写出(a+b)2展开式所缺的系数
仔细观察三角系数表,按规律写出(a+b)2展开式所缺的系数